Lately, linear discrete-time control theory has start to appear in areas far beyond the ordinary. As a byproduct, papers start to surface which claim that stability of linear discrete-time systems
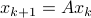
is characterized by 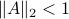 .
The confunsion is complete by calling this object the spectral norm of a matrix
.
The confunsion is complete by calling this object the spectral norm of a matrix 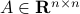 .
Indeed, for fixed coordinates, stability of
.
Indeed, for fixed coordinates, stability of  is not characterized by
is not characterized by 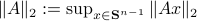 , but by
, but by ![rho(A):=max_{iin [n]}|lambda_i(A)|](eqs/8716262940618826552-130.png) .
If
.
If 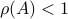 , then, all absolute eigenvalues of
, then, all absolute eigenvalues of  are strictly smaller than one, and hence for
are strictly smaller than one, and hence for 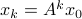 ,
, 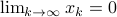 .
This follows from the Jordan form of
.
This follows from the Jordan form of  in combination with the simple observation that for
in combination with the simple observation that for 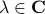 ,
, 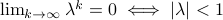 .
.
To continue, define two sets; 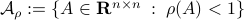 and
and 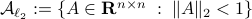 .
Since
.
Since![^{[1]}](eqs/2708305882951756665-130.png)
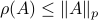 we have
we have 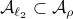 . Now, the main question is, how much do we lose by approximating
. Now, the main question is, how much do we lose by approximating  with
with 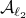 ? Motivation to do so is given by the fact that
? Motivation to do so is given by the fact that 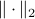 is a norm and hence a convex function
is a norm and hence a convex function![^{[2]}](eqs/2708306882823756034-130.png) , i.e., when given a convex polytope
, i.e., when given a convex polytope 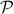 with vertices
with vertices 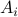 , if
, if 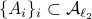 , then
, then 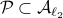 . Note that
. Note that 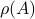 is not a norm,
is not a norm, 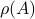 can be
can be  without
without 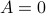 (consider an upper-triangular matrix with zeros on the main diagonal), the triangle inequality can easily fail as well. For example, let
(consider an upper-triangular matrix with zeros on the main diagonal), the triangle inequality can easily fail as well. For example, let
![A_1 = left[begin{array}{ll} 0 & 1 0 & 0 end{array}right], quad A_2 = left[begin{array}{ll} 0 & 0 1 & 0 end{array}right],](eqs/6730715665771009175-130.png)
Then 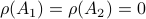 , but
, but 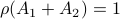 , hence
, hence 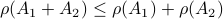 fails to hold.
A setting where the aforementioned property of
fails to hold.
A setting where the aforementioned property of 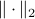 might help is Robust Control, say we want to assess if some algorithm rendered a compact convex set
might help is Robust Control, say we want to assess if some algorithm rendered a compact convex set  , filled with
, filled with  's, stable.
As highlighted before, we could just check if all extreme points of
's, stable.
As highlighted before, we could just check if all extreme points of  are members of
are members of 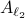 , which might be a small and finite set.
Thus, computationally, it appears to be attractive to consider
, which might be a small and finite set.
Thus, computationally, it appears to be attractive to consider 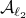 over the generic
over the generic  .
.
As a form of critique, one might say that  is a lot larger than
is a lot larger than 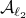 .
Towards such an argument, one might recall that
.
Towards such an argument, one might recall that 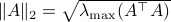 . Indeed,
. Indeed, 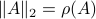 if
if![^{[3]}](eqs/2708307882947756447-130.png)
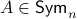 , but
, but 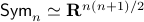 . Therefore, it seems like the set of
. Therefore, it seems like the set of  for which considering
for which considering 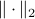 over
over 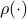 is reasonable, is negligibly small.
To say a bit more, since
is reasonable, is negligibly small.
To say a bit more, since![^{[4]}](eqs/2708308882819756064-130.png)
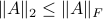 we see that we can always find a ball with non-zero volume fully contained in
we see that we can always find a ball with non-zero volume fully contained in  .
Hence,
.
Hence,  is at least locally dense in
is at least locally dense in 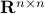 .
So in principle we could try to investigate
.
So in principle we could try to investigate 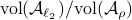 . For
. For 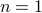 , the sets agree, which degrades asymptotically.
However, is this the way to go? Lets say we consider the set
, the sets agree, which degrades asymptotically.
However, is this the way to go? Lets say we consider the set 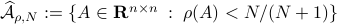 . Clearly, the sets
. Clearly, the sets 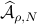 and
and  are different, even in volume, but for sufficiently large
are different, even in volume, but for sufficiently large 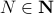 , should we care? The behaviour they parametrize is effectively the same.
, should we care? The behaviour they parametrize is effectively the same.
We will stress that by approximating  with
with 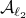 , regardless of their volumetric difference, we are ignoring a full class of systems and miss out on a non-neglible set of behaviours.
To see this, any system described by
, regardless of their volumetric difference, we are ignoring a full class of systems and miss out on a non-neglible set of behaviours.
To see this, any system described by 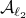 is contractive in the sense that
is contractive in the sense that 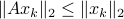 , while systems in
, while systems in  are merely asymptotically stable. They might wander of before they return, i.e., there is no reason why for all
are merely asymptotically stable. They might wander of before they return, i.e., there is no reason why for all 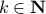 we must have
we must have 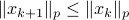 . We can do a quick example, consider the matrices
. We can do a quick example, consider the matrices
![A_2 = left[begin{array}{lll} 0 & -0.9 & 0.1 0.9 & 0 & 0 0 & 0 & -0.9 end{array}right], quad A_{rho} = left[begin{array}{lll} 0.1 & -0.9 & 1 0.9 & 0 & 0 0 & 0 & -0.9 end{array}right].](eqs/7939256391259616851-130.png)
Then 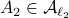 ,
, 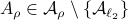 and both
and both 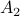 and
and 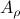 have
have 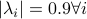 .
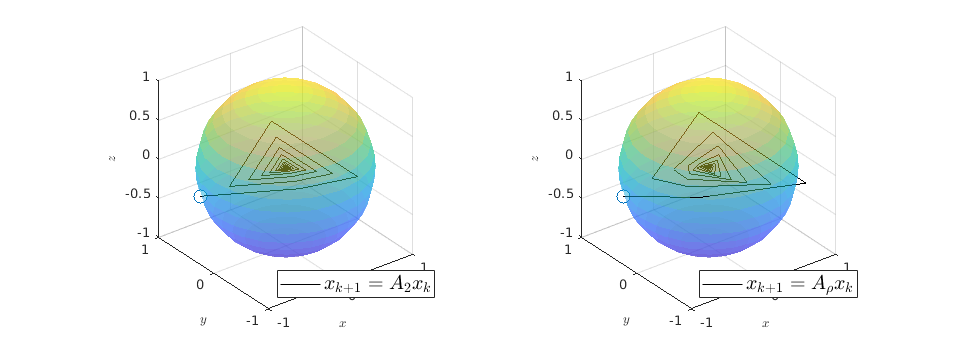
We observe that indeed
.
We observe that indeed 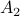 is contractive, for any initial condition on
is contractive, for any initial condition on 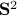 , we move strictly inside the sphere, whereas for
, we move strictly inside the sphere, whereas for 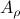 , when starting from the same initial condition, we take a detour outside of the sphere before converging to
, when starting from the same initial condition, we take a detour outside of the sphere before converging to  . So although
. So although 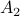 and
and 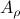 have the same spectrum, they parametrize different systems.
have the same spectrum, they parametrize different systems.
 |
In our deterministic setting this would mean that we would confine our statespace to a (solid) sphere with radius 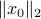 , instead of
, instead of 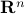 .
Moreover, in linear optimal control, the resulting closed-loop system is usually not contractive.
Think of the infamous pendulum on a cart. Being energy efficient has usually nothing to do with taking the shortest, in the Euclidean sense, path.
.
Moreover, in linear optimal control, the resulting closed-loop system is usually not contractive.
Think of the infamous pendulum on a cart. Being energy efficient has usually nothing to do with taking the shortest, in the Euclidean sense, path.
(update June 06): As suggested by Pedro Zattoni, we would like to add some nuance here. As highlighted in the first 12 minutes of this lecture by Pablo Parrilo, if  is stable, then, one can always find a (linear) change of coordinates such that the transformed system matrix is contractive. Although a very neat observation, you have to be careful, since your measurements might not come from this transformed system. So either you assume merely that
is stable, then, one can always find a (linear) change of coordinates such that the transformed system matrix is contractive. Although a very neat observation, you have to be careful, since your measurements might not come from this transformed system. So either you assume merely that  is stable, or you assume that
is stable, or you assume that  is contractive, but then you might need to find an additional map, mapping your states to your measurements.
is contractive, but then you might need to find an additional map, mapping your states to your measurements.
![[1]](eqs/8209412804330245758-130.png) : Recall,
: Recall, 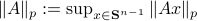 . Then, let
. Then, let 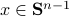 be some eigenvector of
be some eigenvector of  . Now we have
. Now we have 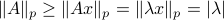 . Since this eigenvalue is arbitrary it follows that
. Since this eigenvalue is arbitrary it follows that 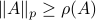 .
.
![[2]](eqs/8209412804333245623-130.png) : Let
: Let 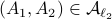 then
then 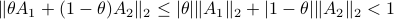 . This follows from the
. This follows from the 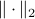 being a norm.
being a norm.
![[3]](eqs/8209412804332245752-130.png) : Clearly, if
: Clearly, if 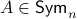 , we have
, we have 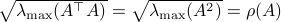 . Now, when
. Now, when 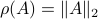 , does this imply that
, does this imply that 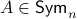 ? The answer is no, consider
? The answer is no, consider
![A' = left[begin{array}{lll} 0.9 & 0 & 0 0 & 0.1 & 0 0 & 0.1 & 0.1 end{array}right].](eqs/1479234184051328788-130.png)
Then, 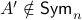 , yet,
, yet, 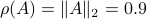 . For the full set of conditions on
. For the full set of conditions on  such that
such that 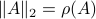 see this paper by Goldberg and Zwas.
see this paper by Goldberg and Zwas.
![[4]](eqs/8209412804335245617-130.png) : Recall that
: Recall that 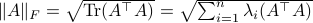 . This expression is clearly larger or equal to
. This expression is clearly larger or equal to 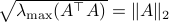 .
.