A Special Group, Volume Preserving Feedback |16 Nov. 2019|
tags: math.LA, math.DS
Let's say we have a  -dimensional linear discrete-time dynamical system
-dimensional linear discrete-time dynamical system 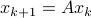 , which preserves the volume of the cube
, which preserves the volume of the cube ![[-1,1]^2](eqs/7220646983027292775-130.png) under the dynamics, i.e.
under the dynamics, i.e. ![mathrm{Vol}([-1,1]^2)=mathrm{Vol}(A^k[-1,1]^2)](eqs/6078350520623442645-130.png) for any
for any 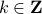 .
.
Formally put, this means that  is part of a certain group, specifically, consider some field
is part of a certain group, specifically, consider some field 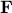 and
define the Special Linear group by
and
define the Special Linear group by
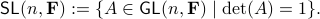
Now, assume that we are only interested in matrices 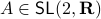 such that the cube
such that the cube ![[-1,1]^2](eqs/7220646983027292775-130.png) remains bounded under the dynamics, i.e.,
remains bounded under the dynamics, i.e., ![lim_{kto infty}A^k[-1,1]^2](eqs/6180125548835686349-130.png) is bounded. In this scenario we restrict our attention to
is bounded. In this scenario we restrict our attention to 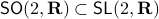 . To see why this is needed, consider
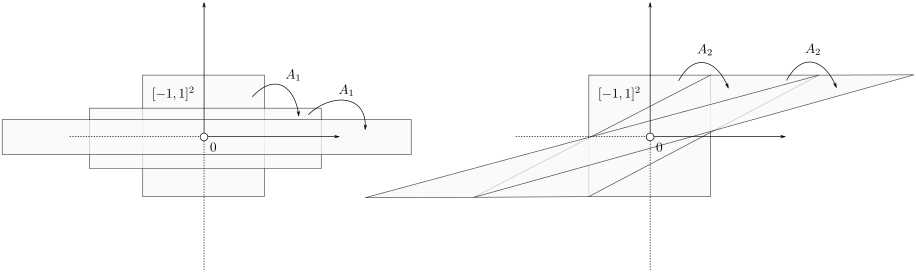
. To see why this is needed, consider 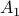 and
and 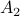 both with determinant
both with determinant  :
:
![A_1 = left[ begin{array}{ll} 2 & 0 0 & frac{1}{2} end{array}right], quad A_2 = left[ begin{array}{ll} 1 & 2 0 & 1 end{array}right],](eqs/4004660008936570769-130.png)
If we look at the image of ![[-1,1]^2](eqs/7220646983027292775-130.png) under both these maps (for several iterations), we see that volume is preserved, but also clearly that the set is extending indefinitely in the horizontal direction.
under both these maps (for several iterations), we see that volume is preserved, but also clearly that the set is extending indefinitely in the horizontal direction.
 |
To have a somewhat interesting problem, assume we are given  with
with  while it is our task to find a
while it is our task to find a  such that
such that 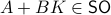 , hence, find feedback which not only preserves the volume, but keeps any set of initial conditions (say
, hence, find feedback which not only preserves the volume, but keeps any set of initial conditions (say ![[-1,1]^2](eqs/7220646983027292775-130.png) ) bounded over time.
) bounded over time.
Towards a solution, we might ask, given any 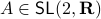 what is the nearest (in some norm) rotation matrix? This turns out to be a classic question, starting from orthogonal matrices, the solution to
what is the nearest (in some norm) rotation matrix? This turns out to be a classic question, starting from orthogonal matrices, the solution to 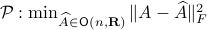 is given by
is given by 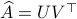 , where
, where 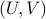 follows from the SVD of
follows from the SVD of  ,
, 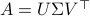 .
Differently put, when we use a polar decomposition of
.
Differently put, when we use a polar decomposition of  ,
, 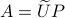 , then the solution is given by
, then the solution is given by 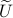 . See this note for a quick multiplier proof.
An interesting sidenote, problem
. See this note for a quick multiplier proof.
An interesting sidenote, problem 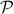 is well-defined since
is well-defined since 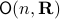 is compact. To see this, recall that for any
is compact. To see this, recall that for any 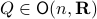 we have
we have 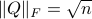 , hence the set is bounded, plus
, hence the set is bounded, plus 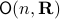 is the pre-image of
is the pre-image of 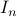 under
under 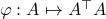 ,
, 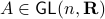 , hence the set is closed as well.
, hence the set is closed as well.
This is great, however, we would like to optimize over 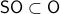 instead. To do so, one usually resorts to simply checking the sign - and if necessary - flipping it via finding the closest matrix with a change in determinant sign.
We will see that by selecting appropriate coordinates we can find the solution without this checking of signs.
instead. To do so, one usually resorts to simply checking the sign - and if necessary - flipping it via finding the closest matrix with a change in determinant sign.
We will see that by selecting appropriate coordinates we can find the solution without this checking of signs.
For today we look at 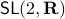 and largely follow (DK1999), for such a
and largely follow (DK1999), for such a  -dimensional matrix, the determinant requirement translates to
-dimensional matrix, the determinant requirement translates to 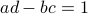 . Under the following (invertible) linear change of coordinates
. Under the following (invertible) linear change of coordinates
![left[ begin{array}{l} a d b c end{array}right] = left[ begin{array}{llll} 1 & 1 & 0 & 0 1 & -1 & 0 & 0 0 & 0 & 1 & 1 0 & 0 & 1 & -1 end{array}right] left[ begin{array}{l} p q r s end{array}right]](eqs/6118233270205082065-130.png)
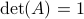 becomes
becomes 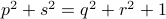 , i.e., for any pair
, i.e., for any pair 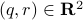 the point
the point 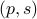 runs over a circle with radius
runs over a circle with radius 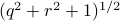 . Hence, we obtain the diffeomorphism
. Hence, we obtain the diffeomorphism 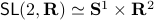 . We can use however a more pretty diffeomorphism of the sphere and an open set in
. We can use however a more pretty diffeomorphism of the sphere and an open set in 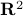 . To that end, use the diffeomorphism:
. To that end, use the diffeomorphism:
![(theta,(u,v)) mapsto frac{1}{sqrt{1-u^2-v^2}} left[ begin{array}{ll} cos(theta)+u & -sin(theta)+v sin(theta)+v & cos(theta)-u end{array}right] in mathsf{SL}(2,mathbf{R}),](eqs/6656969251929689946-130.png)
for 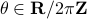 (formal way of declaring that
(formal way of declaring that 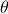 should not be any real number) and the pair
should not be any real number) and the pair 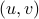 being part of
being part of 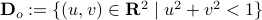 (the open unit-disk).
To see this, recall that the determinant is not a linear operator.
Since we have a
(the open unit-disk).
To see this, recall that the determinant is not a linear operator.
Since we have a  -dimensional example we can explicitly compute the eigenvalues of any
-dimensional example we can explicitly compute the eigenvalues of any 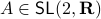 (plug
(plug 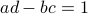 into the characteristic equation) and obtain:
into the characteristic equation) and obtain:
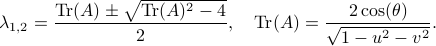
At this point, the only demand on the eigenvalues is that 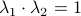 . Therefore, when we would consider
. Therefore, when we would consider  within the context of a discrete linear dynamical system
within the context of a discrete linear dynamical system 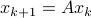 ,
,  is either a saddle-point, or we speak of a marginally stable system (
is either a saddle-point, or we speak of a marginally stable system (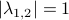 ).
We can visualize the set of all marginally stable
).
We can visualize the set of all marginally stable 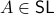 , called
, called 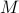 , defined by all
, defined by all 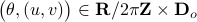 satisfying
satisfying
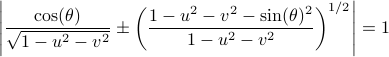
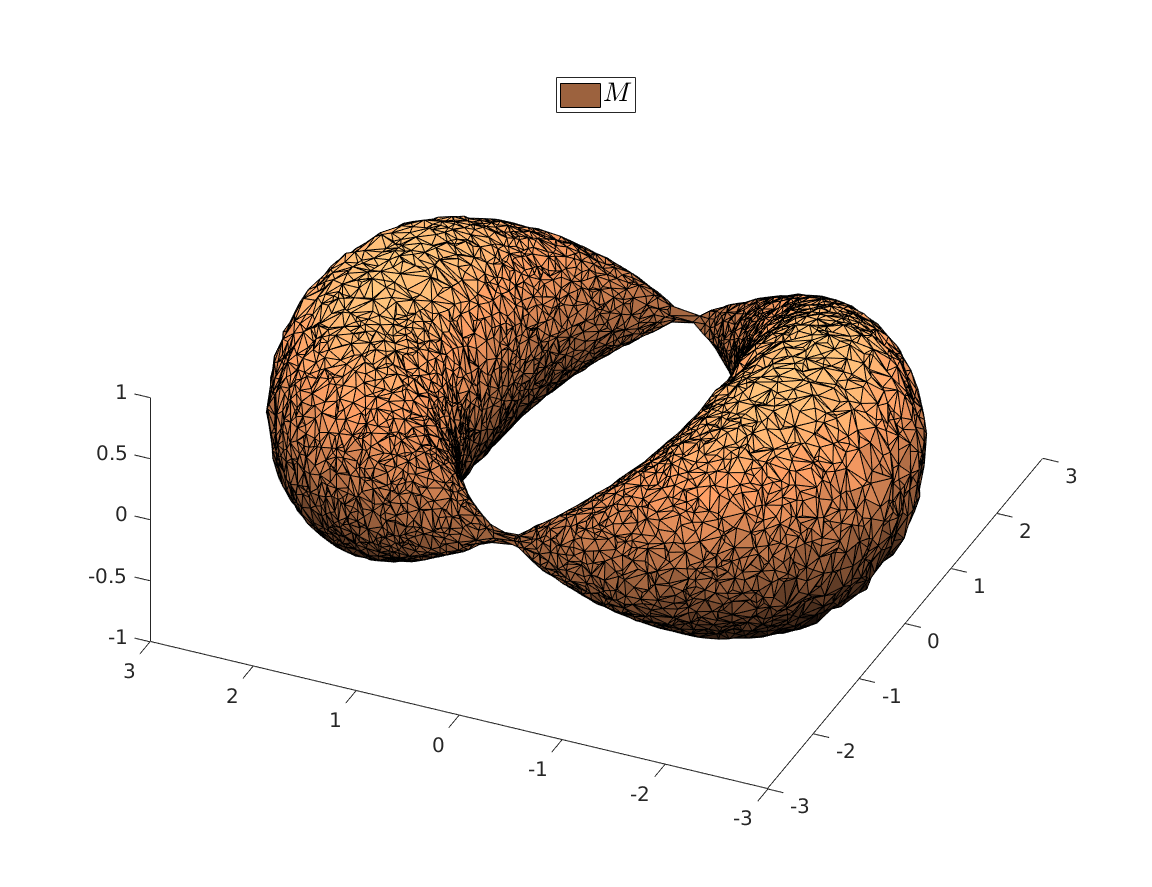 |
Once we visualize |
To find close (in Frobenius-norm) rotation matrices, given any 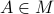 , we observe that we can do the Polar decomposition
, we observe that we can do the Polar decomposition 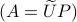 explicitly in
explicitly in 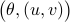 coordinates, given any
coordinates, given any 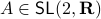 we get
we get 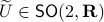 (standard rotation matrix parametrized by
(standard rotation matrix parametrized by 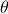 ) plus a symmetric positive definite
) plus a symmetric positive definite 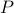 , defined by:
, defined by:
![P = frac{1}{sqrt{1-u^2-v^2}} left[ begin{array}{ll} 1+cos(theta) u + sin(theta)v & cos(theta)v-sin(theta)u cos(theta)v-sin(theta)u & 1-sin(theta)v-cos(theta)u end{array}right].](eqs/2836384178598502055-130.png)
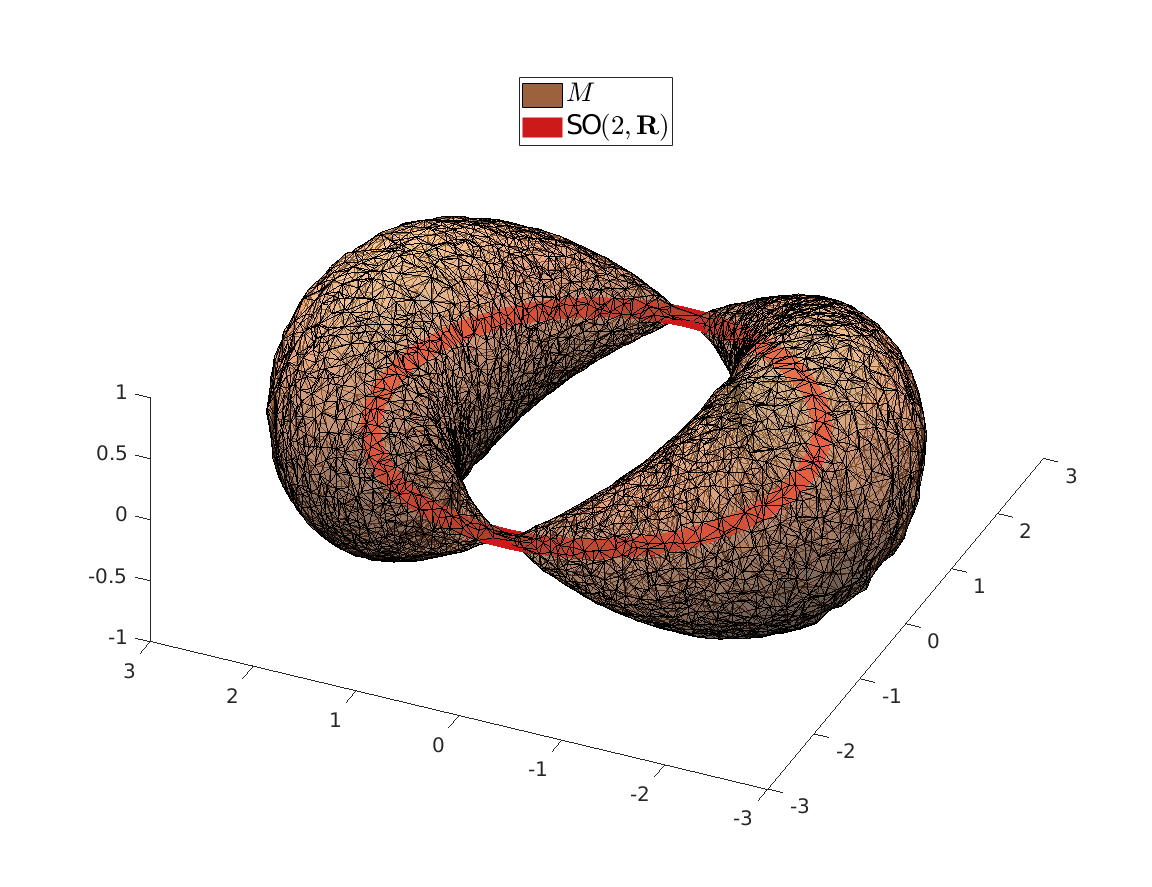 |
It turns out that all these |
As a last step, given an approximation 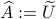 to
to  , can we find a control gain
, can we find a control gain  such that
such that  is (efficiently) generated by
is (efficiently) generated by 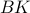 . If we assume that
. If we assume that 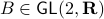 , the solution is given by
, the solution is given by 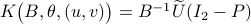 . So, if
. So, if  was already a rotation matrix, then
was already a rotation matrix, then 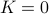 indeed.
indeed.
(DK1999) J.J. Duistermaat and J.A.C. Kolk : ‘‘Lie Groups’’, 1999 Springer.
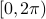 ), then this set
), then this set 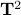 . Note that
. Note that 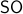 since we still contain matrices like
since we still contain matrices like