Co-observability |6 January 2022|
tags: math.OC
A while ago Prof. Jan H. van Schuppen published his book Control and System Theory of Discrete-Time Stochastic Systems. In this post I would like to highlight one particular concept from the book: (stochastic) co-observability, which is otherwise rarely discussed.
We start with recalling observability. Given a linear-time-invariant system with 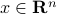 ,
, 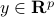 :
:
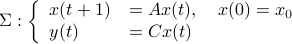
one might wonder if the initial state 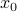 can be recovered from a sequence of outputs
can be recovered from a sequence of outputs  . (This is of great use in feedback problems.) By observing that
. (This is of great use in feedback problems.) By observing that 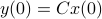 ,
, 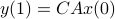 ,
, 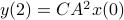 one is drawn to the observability matrix
one is drawn to the observability matrix
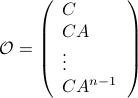
Without going into detectability, when 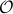 is full-rank, one can (uniquely) recover
is full-rank, one can (uniquely) recover 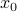 (proof by contradiction). If this is the case, we say that
(proof by contradiction). If this is the case, we say that  , or equivalenty the pair
, or equivalenty the pair 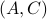 , is observable. Note that using a larger matrix (more data) is redudant by the Cayley-Hamilton theorem (If
, is observable. Note that using a larger matrix (more data) is redudant by the Cayley-Hamilton theorem (If 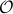 would not be full-rank, but by adding
would not be full-rank, but by adding 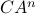 “from below” it would somehow be full-rank, one would contradict the Cayley-Hamilton theorem.).
Also note that in practice one does not “invert”
“from below” it would somehow be full-rank, one would contradict the Cayley-Hamilton theorem.).
Also note that in practice one does not “invert” 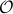 but rather uses a (Luenberger) observer (or a Kalman filter).
but rather uses a (Luenberger) observer (or a Kalman filter).
Now lets continue with a stochastic (Gaussian) system, can we do something similar? Here it will be even more important to only think about observability matrices as merely tools to assert observability. Let 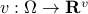 be a zero-mean Gaussian random variable with covariance
be a zero-mean Gaussian random variable with covariance 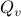 and define for some matrices
and define for some matrices 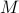 and
and  the stochastic system
the stochastic system
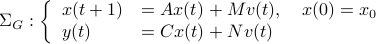
We will assume that  is asymptotically (exponentially stable) such that the Lyapunov equation describing the (invariant) state-covariance is defined:
is asymptotically (exponentially stable) such that the Lyapunov equation describing the (invariant) state-covariance is defined:
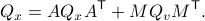
Now the support of the state 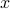 is the range of
is the range of 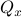 .
.
A convenient tool to analyze 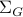 will be the characteristic function of a Gaussian random variable
will be the characteristic function of a Gaussian random variable  , defined as
, defined as ![varphi(omega)=mathbf{E}[mathrm{exp}(ilangle omega, Xrangle)]](eqs/1509536698066778096-130.png) .
It can be shown that for a Gaussian random variable
.
It can be shown that for a Gaussian random variable 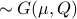
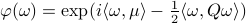 .
With this notation fixed, we say that
.
With this notation fixed, we say that  is stochastically observable on the internal
is stochastically observable on the internal  if the map
if the map
![x(t)mapsto mathbf{E}[mathrm{exp}(ilangle omega,bar{y}rangle|mathcal{F}^{x(t)}],quad bar{y}=(y(t),dots,y(t+k))in mathbf{R}^{pcdot(k+1)}quad forall omega](eqs/853891715523836887-130.png)
is injective on the support of  (note the
(note the 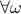 ). The intuition is the same as before, but now we want the state to give rise to an unique (conditional) distribution. At this point is seems rather complicated, but as it turns out, the conditions will be similar to ones from before. We start by writing down explicit expressions for
). The intuition is the same as before, but now we want the state to give rise to an unique (conditional) distribution. At this point is seems rather complicated, but as it turns out, the conditions will be similar to ones from before. We start by writing down explicit expressions for 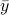 , as
, as
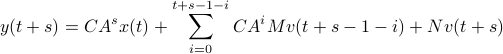
we find that
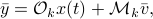
for 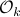 the observability matrix corresponding to the data (length) of
the observability matrix corresponding to the data (length) of 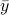 ,
, 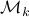 a matrix containing all the noise related terms and
a matrix containing all the noise related terms and 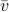 a stacked vector of noises similar to
a stacked vector of noises similar to 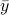 . It follows that
. It follows that ![x(t)mapsto mathbf{E}[mathrm{exp}(ilangle omega,bar{y})|mathcal{F}^{x(t)}]](eqs/1452358234763943133-130.png) is given by
is given by 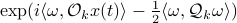 , for
, for ![mathcal{Q}_k = mathbf{E}[mathcal{M}_kbar{v}bar{v}^{mathsf{T}}mathcal{M}_k^{mathsf{T}}]](eqs/8712945555052273745-130.png) . Injectivity of this map clearly relates directly to injectivity of
. Injectivity of this map clearly relates directly to injectivity of 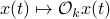 . As such (taking the support into account), a neat characterization of stochastic observability is that
. As such (taking the support into account), a neat characterization of stochastic observability is that 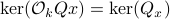 .
.
Then, to introduce the notion of stochastic co-observability we need to introduce the backward representation of a system. We term system representations like 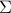 and
and 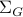 “forward” representations as
“forward” representations as 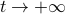 . Assume that
. Assume that 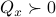 , then see that the forward representation of a system matrix, denoted
, then see that the forward representation of a system matrix, denoted 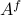 is given by
is given by ![A^f = mathbf{E}[x(t+1)x(t)^{mathsf{T}}]Q_x^{-1}](eqs/3247376240463532393-130.png) . In a similar vein, the backward representation is given by
. In a similar vein, the backward representation is given by ![A^b=mathbf{E}[x(t-1)x(t)^{mathsf{T}}]Q_x^{-1}](eqs/3587697042984921977-130.png) .
Doing the same for the output matrix
.
Doing the same for the output matrix 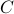 yields
yields ![C^b=mathbf{E}[y(t-1)x(t)^{mathsf{T}}]Q_x^{-1}](eqs/2184503885116254462-130.png) and thereby the complete backward system
and thereby the complete backward system
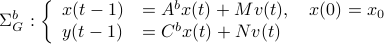
Note, to keep 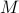 and
and  fixed, we adjust the distribution of
fixed, we adjust the distribution of  .
Indeed, when
.
Indeed, when 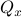 is not full-rank, the translation between forward and backward representations is not well-defined. Initial conditions
is not full-rank, the translation between forward and backward representations is not well-defined. Initial conditions 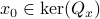 cannot be recovered.
cannot be recovered.
To introduce co-observability, ignore the noise for the moment and observe that 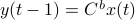 ,
, 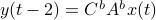 , and so forth.
We see that when looking at observability using the backward representation, we can ask if it possible to recover the current state using past outputs. Standard observability looks at past states instead. With this in mind we can define stochastic co-observability on the interval
, and so forth.
We see that when looking at observability using the backward representation, we can ask if it possible to recover the current state using past outputs. Standard observability looks at past states instead. With this in mind we can define stochastic co-observability on the interval 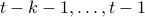 be demanding that the map
be demanding that the map
![x(t)mapsto mathbf{E}[mathrm{exp}(ilangle omega,bar{y}^brangle|mathcal{F}^{x(t)}],quad bar{y}^b=(y(t-1),dots,y(t-k-1))in mathbf{R}^{pcdot(k+1)}quad forall omega](eqs/2807210638750947645-130.png)
is injective on the support of 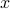 (note the
(note the 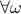 ). Of course, one needs to make sure that
). Of course, one needs to make sure that 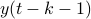 is defined. It is no surprise that the conditions for stochastic co-observability will also be similar, but now using the co-observability matrix. What is however remarkable, is that these notions do not always coincide.
is defined. It is no surprise that the conditions for stochastic co-observability will also be similar, but now using the co-observability matrix. What is however remarkable, is that these notions do not always coincide.
Lets look at when this can happen and what this implies. One reason to study these kind of questions is to say something about (minimal) realizations of stochastic processes. Simply put, what is the smallest (as measured by the dimension of the state 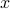 ) system
) system 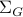 that gives rise to a certain output process. When observability and co-observability do not agree, this indicates that the representation is not minimal. To get some intuition, we can do an example as adapted from the book. Consider the scalar (forward) Gaussian system
that gives rise to a certain output process. When observability and co-observability do not agree, this indicates that the representation is not minimal. To get some intuition, we can do an example as adapted from the book. Consider the scalar (forward) Gaussian system
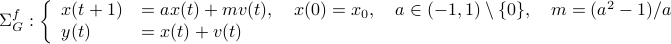
for 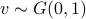 . The system is stochastically observable as
. The system is stochastically observable as 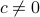 and
and 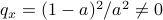 . Now for stochastic co-observability we see that
. Now for stochastic co-observability we see that ![c^b=mathbf{E}[y(t-1)x(t)]q_x^{-1}]=0](eqs/6755659394537019237-130.png) , as such the system is not co-observable. What this shows is that
, as such the system is not co-observable. What this shows is that 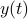 behaves as a Gaussian random variable, no internal dynamics are at play and such a minimal realization is of dimension
behaves as a Gaussian random variable, no internal dynamics are at play and such a minimal realization is of dimension 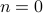 .
.
For this and a lot more, have a look at the book!