Finite Calls to Stability | 31 Oct. 2019 |
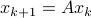 parametrized by
parametrized by 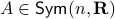 .
In this short note we look at a relatively simple, yet neat method to assess stability of
.
In this short note we look at a relatively simple, yet neat method to assess stability of  via finite calls to a particular oracle. Here, we will follow the notes by Roman Vershynin (RV2011).
via finite calls to a particular oracle. Here, we will follow the notes by Roman Vershynin (RV2011). Assume we have no knowledge of  , but we are able to obtain
, but we are able to obtain 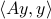 for any desired
for any desired 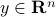 . It turns out that we can use this oracle to bound
. It turns out that we can use this oracle to bound 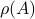 from above.
from above.
First, recall that since  is symmetric,
is symmetric, 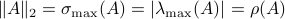 . Now, the common definition of
. Now, the common definition of 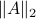 is
is 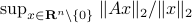 . The constraint set
. The constraint set 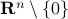 is not per se convenient from a computational point of view. Instead, we can look at a compact constraint set:
is not per se convenient from a computational point of view. Instead, we can look at a compact constraint set: 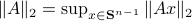 , where
, where 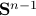 is the sphere in
is the sphere in 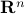 .
The latter formulation has an advantage, we can discretize these compact constraints sets and tame functions over the individual chunks.
.
The latter formulation has an advantage, we can discretize these compact constraints sets and tame functions over the individual chunks.
To do this formally, we can use  -nets, which are convenient in quantitative analysis on compact metric spaces
-nets, which are convenient in quantitative analysis on compact metric spaces 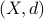 . Let
. Let 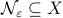 be a
be a  -net for
-net for  if
if 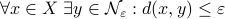 . Hence, we measure the amount of balls to cover
. Hence, we measure the amount of balls to cover  .
.
For example, take 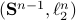 as our metric space where we want to bound
as our metric space where we want to bound 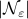 (the cardinality, i.e., the amount of balls). Then, to construct a minimal set of balls, consider an
(the cardinality, i.e., the amount of balls). Then, to construct a minimal set of balls, consider an  -net of balls
-net of balls 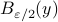 , with
, with 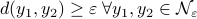 . Now the insight is simply that
. Now the insight is simply that 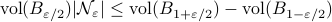 .
Luckily, we understand the volume of
.
Luckily, we understand the volume of 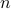 -dimensional Euclidean balls well such that we can establish
-dimensional Euclidean balls well such that we can establish
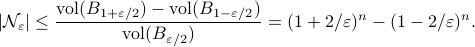
Which is indeed sharper than the bound from Lemma 5.2 in (RV2011).
Next, we recite Lemma 5.4 from (RV2011). Given an  -net for
-net for 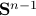 with
with  we have
we have
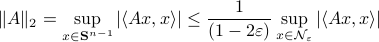
This can be shown using the Cauchy-Schwartz inequality. Now, it would be interesting to see how sharp this bound is.
To that end, we do a  -dimensional example (
-dimensional example (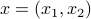 ). Note, here we can easily find an optimal grid using polar coordinates. Let the unknown system be parametrized by
). Note, here we can easily find an optimal grid using polar coordinates. Let the unknown system be parametrized by
![A = left[ begin{array}{ll} 0.1 & -0.75 -0.75 & 0.1 end{array}right]](eqs/8870555444473195760-130.png)
such that 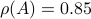 . In the figures below we compute the upper-bound to
. In the figures below we compute the upper-bound to 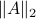 for several nets
for several nets 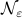 .
Indeed, for finer nets, we see the upper-bound approaching
.
Indeed, for finer nets, we see the upper-bound approaching 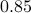 . However, we see that the convergence is slow while being inversely related to the exponential growth in
. However, we see that the convergence is slow while being inversely related to the exponential growth in 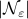 .
.
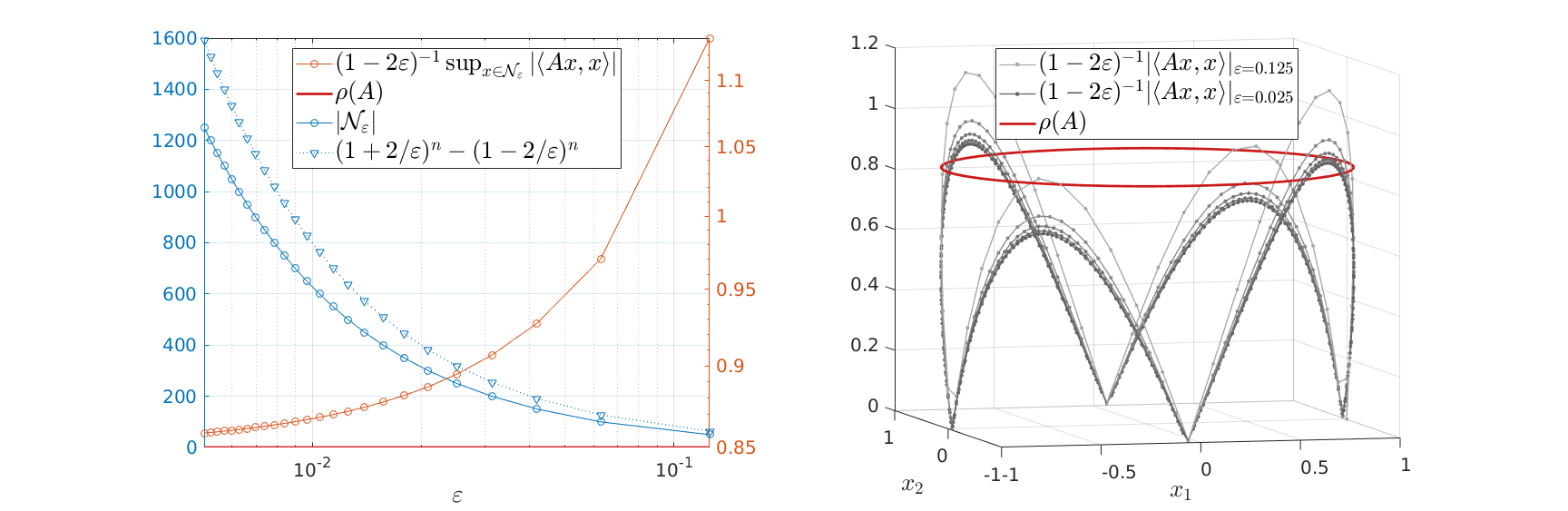 |
Overall, we see that after about a 100 calls to our oracle we can be sure about  being exponentially stable.
Here we just highlighted an example from (RV2011), at a later moment we will discuss its use in probability theory.
being exponentially stable.
Here we just highlighted an example from (RV2011), at a later moment we will discuss its use in probability theory.