On topological properties of closed attractors.
Previously we studied when compact asymptotically stable attractors are homotopy equivalent to their basin of attraction. Interesting work by Lin, Yao and Cao was the motivation to look at closed attractors that need not be compact.
You might have seen definitions of asymptotic stability using norms, metrics or general neighbourhoods. These definitions are not always equivalent and especially when we move beyond compactness this becomes apparent. When working with closed attractors, one is quickly drawn to the metrical definition of stability to have reasonable continuous (converse) Lyapunov theory. However, compared to the compact case, it becomes harder to study topological properties of the attractor and its basin of attraction. A picture to have in mind is shown below.
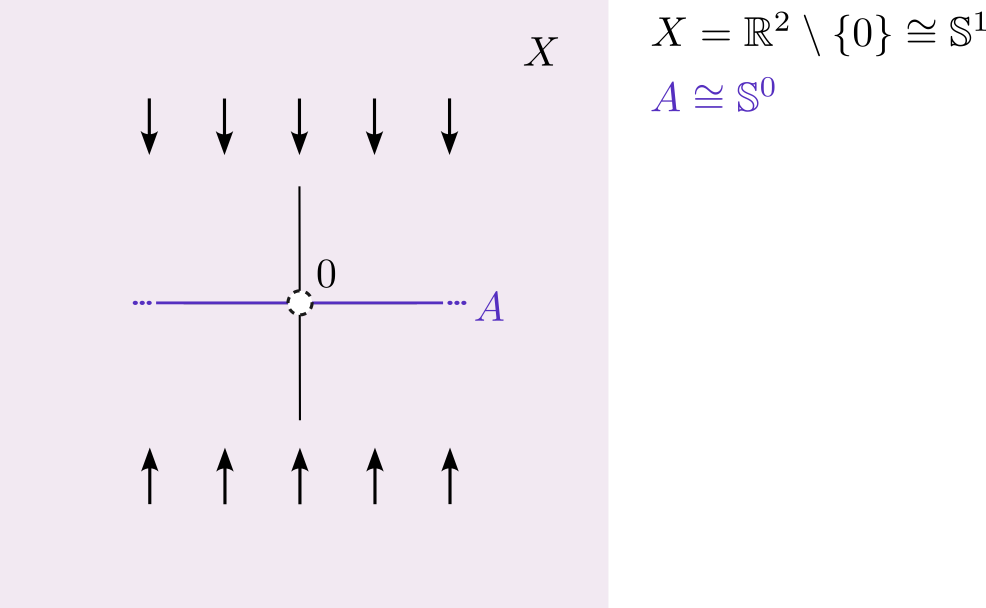
The circular example (Sec. 4.1) from Lin, Yao and Cao is similar but particularly nice as it is less obviously non-compact. Note, they also provide an example (Sec. 4.2) on a complete space, this is very interesting as you might think that a lack of completeness is the crux here.
The picture from above shows how merely closed attractors and their basin of attraction need not have the same homotopy type, this is captured in our new preprint using a minor adaptation of cofibrations. Very simply put, we must enforce that we deform through a metric neighbourhood, not just any neighbourhood. In particular, we capture when homotopy equivalence does hold, which opens the door for further analyis. Let me stress that we build upon on host of beautiful work, do have a look at the books (all of them) by Nemytskii, Stepanov, Bhatia, Szego, Hajek and Zubov, as contained in the bibliography of the preprint. Additionally, have a look at Auslander's work on stability through filters.