Are Theo Jansen his Linkages Optimal? |16 Dec. 2019|
To that end, consider just 1 leg, 1 linkage system as in the figure(s) below. We can write down an explicit expression for 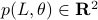 where
where 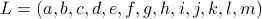 and
and 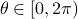 . See below for an explicit derivation. Now, with his motivation in mind, what would be an easy and relevant cost function? An idea is to maximize the ratio
. See below for an explicit derivation. Now, with his motivation in mind, what would be an easy and relevant cost function? An idea is to maximize the ratio 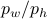 , of course, subject to still having a functioning leg. To that end we consider the cost function (see the schematic below for notation):
, of course, subject to still having a functioning leg. To that end we consider the cost function (see the schematic below for notation):
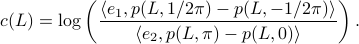
Of course, this is a heuristic, but the intuition is that this should approximate 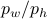 .
Let
.
Let 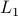 be the set of parameters as given in Jansen his video, then we apply a few steps of (warm-start) gradient ascent:
be the set of parameters as given in Jansen his video, then we apply a few steps of (warm-start) gradient ascent: 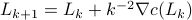 ,
, 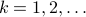 .
.
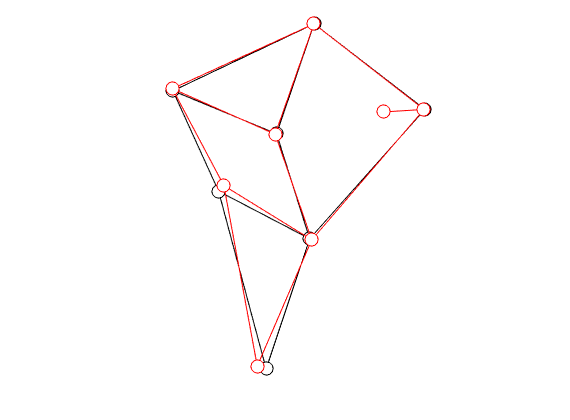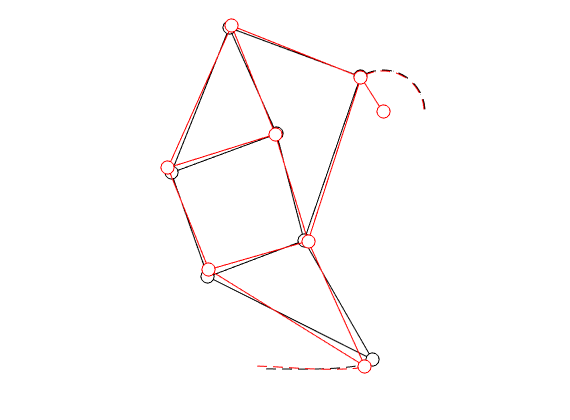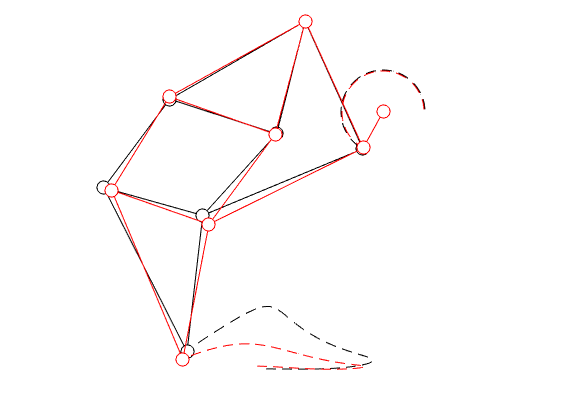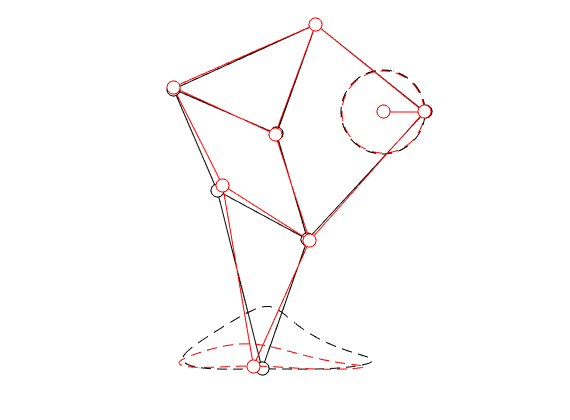 |
In the figure on the left we compare the linkage as given by Jansen (in black) with the result of just two steps of gradient ascent (in red).
You clearly see that the trajectory of the foot becomes more shallow. Nevertheless, we see that the profile starts to become curved on the bottom. It is actually interesting to note that |
Can we conclude anything from here? I would say that we need dynamics, not just kinematics, but more importantly, we need to put the application in the optimization and only Theo Jansen understands the constraints of the beach.
Still, it is fun to see for yourself how this works and like I did you can build a (baby) strandbeest yourself using nothing more than some PVC tubing and a source of heat.
Derivation of  :
:
Essentially, all that you need is the cosine-rule plus some feeling for how to make the equations continuous.
To start, let  and
and  (just the standard unit vectors), plus let
(just the standard unit vectors), plus let 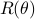 be a standard (counter-clockwise) rotation matrix acting on
be a standard (counter-clockwise) rotation matrix acting on 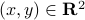 . To explain the main approach, when we want to find the coordinates of for example point
. To explain the main approach, when we want to find the coordinates of for example point 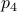 , we try to compute the angle
, we try to compute the angle 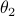 such that when we rotate the unit vector
such that when we rotate the unit vector 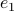 with length
with length 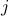 emanating from point
emanating from point 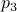 , we get point
, we get point 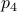 . See the schematic picture below.
. See the schematic picture below.
Then we easily obtain 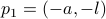 ,
, 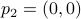 and
and 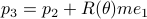 .
Now, to obtain
.
Now, to obtain 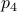 and
and 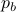 compute the length of the diagonal,
compute the length of the diagonal, 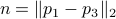 and using the cosine rule
and using the cosine rule 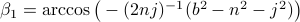 ,
, 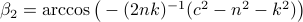 . Then, the trick is to use
. Then, the trick is to use 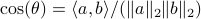 to compute
to compute 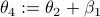 . To avoid angles larger than
. To avoid angles larger than 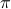 , consider an inner product with
, consider an inner product with 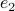 and add the remaining
and add the remaining 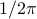 ;
; 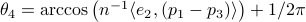 . From there we get
. From there we get 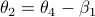 ,
, 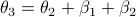 ,
, 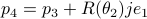 ,
, 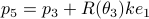 . The point
. The point  is not missing, to check your code it is convenient to compute
is not missing, to check your code it is convenient to compute 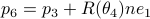 and check that
and check that 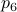 agrees with
agrees with 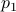 for all
for all 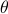 .
In a similar fashion,
.
In a similar fashion, 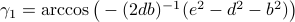 ,
, 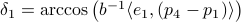 ,
, 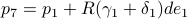 .
Then, for
.
Then, for 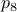 , again compute a diagonal
, again compute a diagonal 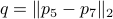 plus
plus 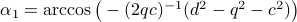 ,
, 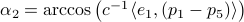
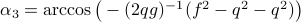 , such that for
, such that for 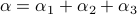 we have
we have 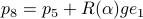 .
At last,
.
At last, 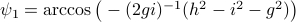 , such that
, such that 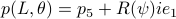 for
for 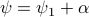 .
.
 |
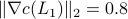 , which is still far from
, which is still far from 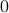 but already remarkably small for
but already remarkably small for 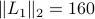 .
.