Simple Flow Algorithm to Compute the Operator Norm |4 Nov. 2019|

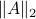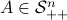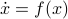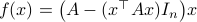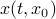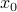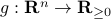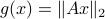Using the ideas from the previous post, we immediately obtain a dynamical system to compute |A|_2 for any $Ain mathcal{S}^n_{++}$ (symmetric positive definite matrices). Here we use the vector field dot{x}=f(x) , defined by $f(x)=big(A-(x^{top}Ax)I_nbig)x$ and denote a solution by x(t,x_0) , where x_0 is the initial condition. Moreover, define a map $g:mathbf{R}^nto mathbf{R}_{geq 0}$ by g(x)=|Ax|_2 . 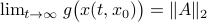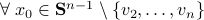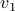Then $lim_{tto infty}gbig(x(t,x_0) big)=|A|_2$ $forall;x_0in mathbf{S}^{n-1}setminus{v_2,dots,v_n}$ , where v_1 is the eigenvector corresponding to the largest eigenvalue.

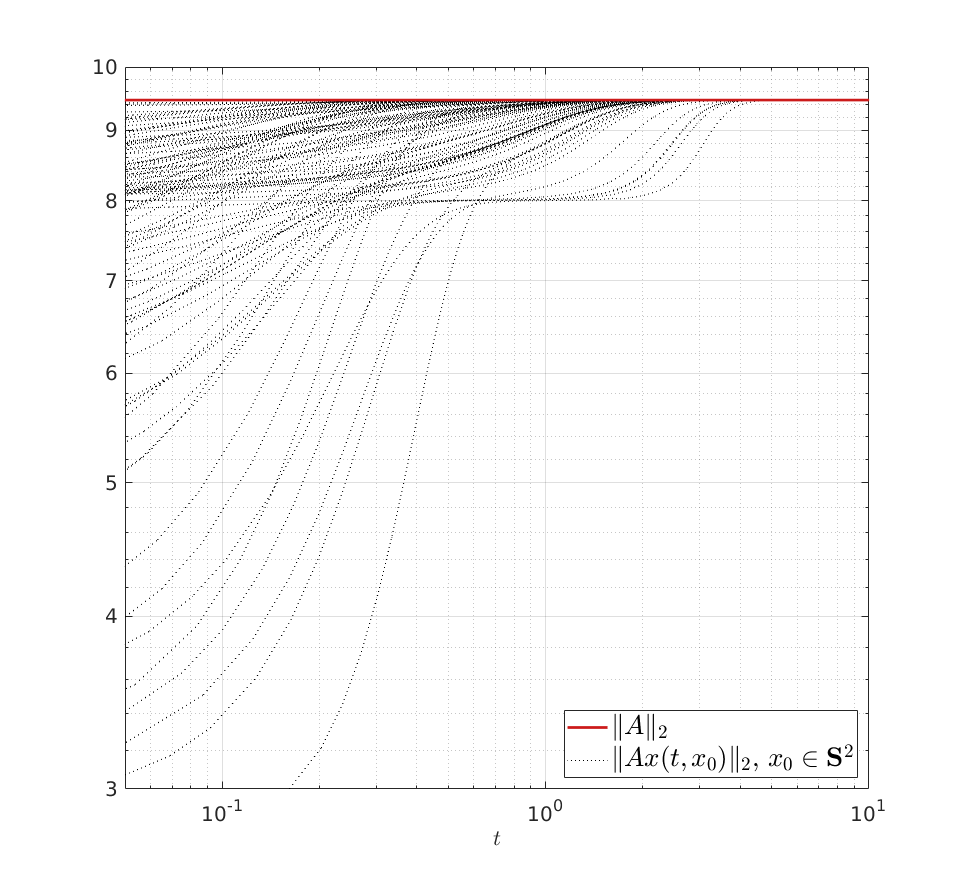We can do a simple example, let

A = left[ begin{array}{lll} 8 & 2 & 0 2 & 4 & 2 0 & 2 & 8 end{array}right]

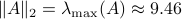with $|A|_2=lambda_{mathrm{max}}(A)approx 9.46$ . Indeed, when given 100 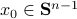$x_0in mathbf{S}^{n-1}$ , we observe convergence. To apply this in practice we obviously need to discretize the flow. To add to that, if we consider the discrete-time version of 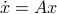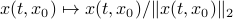dot{x}=Ax , x(t,x_0)mapsto x(t,x_0)/|x(t,x_0)|_2 we can get something of the form 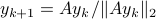$y_{k+1}=Ay_k/|Ay_k|_2$ , which is indeed the Power Iteration algorithm, used to compute the largest eigenvalue of . Recall however that this algorithm needs stronger conditions (on x_0 ) to work than our flow.