Dynamical Systems on the Sphere |3 Nov. 2019|
tags: math.DS
 |
In this post we start a bit with control of systems living on compact metric spaces. This is interesting since we have to rethink what we want, |
To start, consider a linear dynamical systems 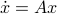 ,
, 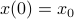 , for which the solution is given by
, for which the solution is given by 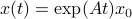 . We can map this solution to the sphere via
. We can map this solution to the sphere via 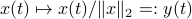 .
The corresponding vector field for
.
The corresponding vector field for 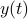 is given by
is given by
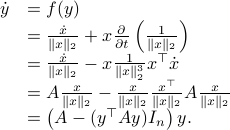
The beauty is the following, to find the equilibria, consider 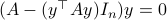 . Of course,
. Of course, 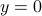 is not valid since
is not valid since 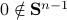 . However, take any eigenvector
. However, take any eigenvector  of
of  , then
, then  is still an eigenvector, plus it lives on
is still an eigenvector, plus it lives on 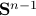 . If we plug such a scaled
. If we plug such a scaled  (from now on consider all eigenvectors to live on
(from now on consider all eigenvectors to live on 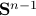 ) into
) into 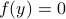 we get
we get 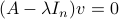 , which is rather cool. The eigenvectors of
, which is rather cool. The eigenvectors of  are (at least) the equilibria of
are (at least) the equilibria of 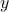 . Note, if
. Note, if 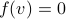 , then so is
, then so is 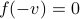 , each eigenvector gives rise to two equilibria.
We say at least, since if
, each eigenvector gives rise to two equilibria.
We say at least, since if 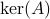 is non-trivial, then for any
is non-trivial, then for any 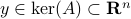 , we get
, we get 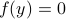 .
.
Let 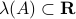 , then what can be said about the stability of the equilibrium points?
Here, we must look at
, then what can be said about the stability of the equilibrium points?
Here, we must look at 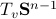 , where the
, where the 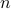 -dimensional system is locally a
-dimensional system is locally a 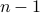 -dimensional linear system. To do this, we start by computing the standard Jacobian of
-dimensional linear system. To do this, we start by computing the standard Jacobian of  , which is given by
, which is given by
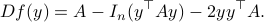
As said before, we do not have a 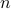 -dimensional system. To that end, we assume
-dimensional system. To that end, we assume 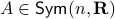 with diagonalization
with diagonalization 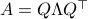 (otherwise perform a Gram-Schmidt procedure) and perform a change of basis
(otherwise perform a Gram-Schmidt procedure) and perform a change of basis 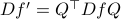 . Then if we are interested in the qualitative stability properties of
. Then if we are interested in the qualitative stability properties of 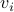 (the
(the 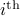 eigenvector of
eigenvector of  ), we can simply look at the eigenvalues of the matrix resulting from removing the
), we can simply look at the eigenvalues of the matrix resulting from removing the 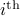 row and column in
row and column in 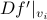 , denoted
, denoted 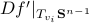 . This seemingly ad hoc construction heavily relies on the embedded structure.
. This seemingly ad hoc construction heavily relies on the embedded structure.
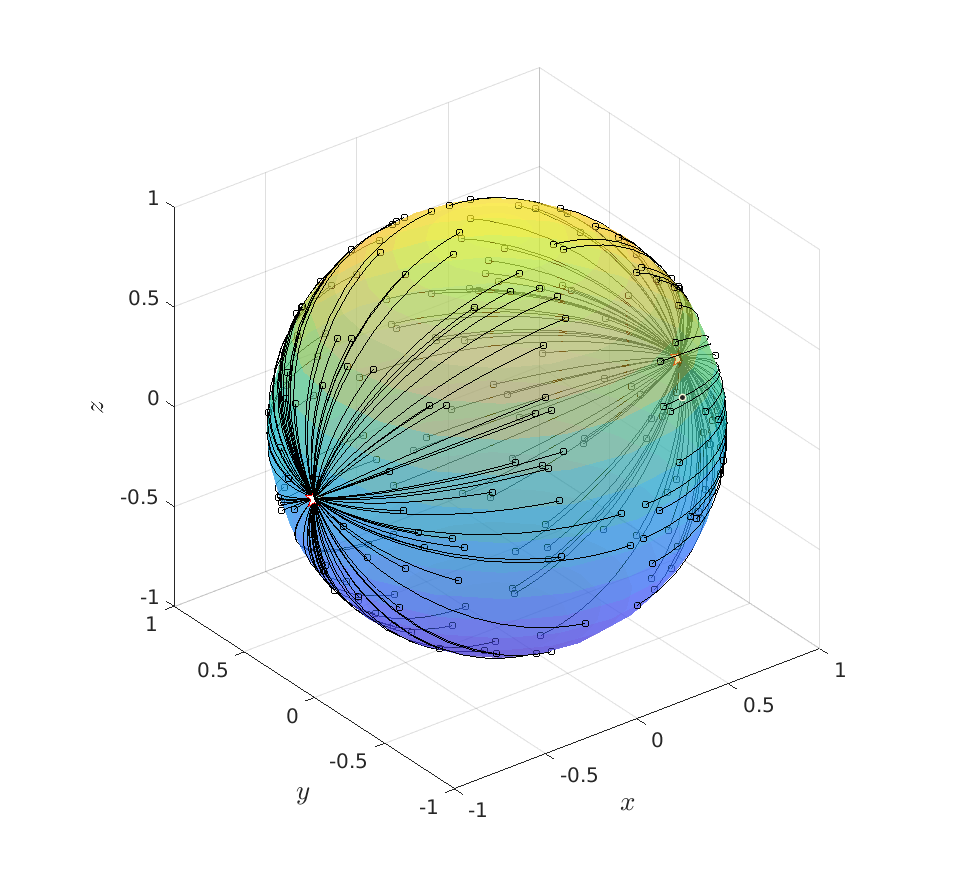
We do two examples. In both figures are the initial conditions indicated with a dot while the equilibrium points are stars.
 |
First, let ![A_1 = left[ begin{array}{lll} 1 & 0 & 0 0 & -1 & 0 0 & 0 & -1 end{array}right]](eqs/4948366788842116208-130.png)
Clearly, for |
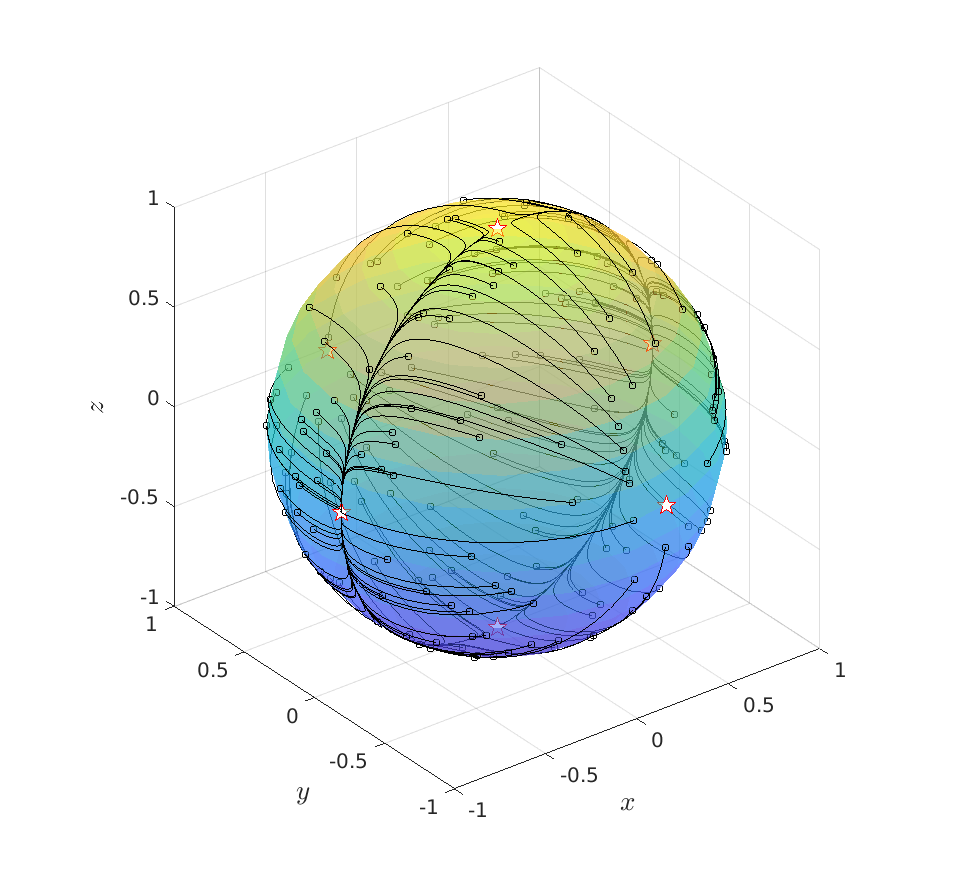 |
Secondly, we consider ![A_2 = left[ begin{array}{lll} 1 & 2 & 0 2 & -10 & 0 0 & 0 & 0.1 end{array}right]](eqs/5655966812910521664-130.png)
To assess stability, we compute ![Df'|_{T_{v_1}mathbf{S}^{2}} = left[ begin{array}{ll} 11.7 & 0 0 & 10.4 end{array}right],quad Df'|_{T_{v_2}mathbf{S}^{2}} = left[ begin{array}{ll} -11.7 & 0 0 & -1.2 end{array}right],quad Df'|_{T_{v_3}mathbf{S}^{2}} = left[ begin{array}{ll} -10.4 & 0 0 & 1.2 end{array}right].](eqs/3105021875749429669-130.png)
Recall that tangent space basis is in line with the eigenvectors plus that the qualitative behaviour around |
Now, a valid question is, why do stable equilibrium points (for 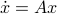 on
on 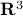 ) become unstable on the sphere?
For our example, we see that the full (minus
) become unstable on the sphere?
For our example, we see that the full (minus  ) line: all
) line: all 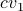 s.t.
s.t. 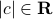 collapses to just two points:
collapses to just two points: 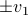 . Not just any two points, but two points surrounded by instability, hence the positive definite Jacobian. In a similar fashion it follows that the unstable asymptotes
. Not just any two points, but two points surrounded by instability, hence the positive definite Jacobian. In a similar fashion it follows that the unstable asymptotes 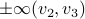 now relate to (finite!) attracting equilibria
now relate to (finite!) attracting equilibria 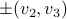 . The fact that
. The fact that 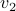 is attracting from all directions while
is attracting from all directions while 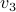 relates to a saddle follows from the corresponding eigenvalues,
relates to a saddle follows from the corresponding eigenvalues, 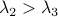 .
From the figure you can take away that
.
From the figure you can take away that 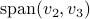 is the attracting plane, resulting in
is the attracting plane, resulting in 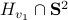 being an attracting great arc (since
being an attracting great arc (since 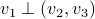 ).
).
We observe that by construction it seems impossible to have 1 stable pole since the equilibrium points come in pairs. You might say, sure, but these vector fields where created by using linear systems. Perhaps there is some wild differential equation which does the trick? The answer is yes, we can however not remove the equilibrium points completely, we cannot comb a hairy ball.
 cannot even occur.
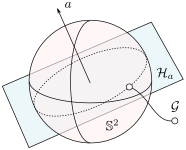
Let a great arc (circle)
cannot even occur.
Let a great arc (circle)  on
on 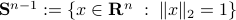 be parametrized by the normal of a hyperplane
be parametrized by the normal of a hyperplane 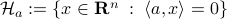 through
through 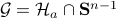 ,
,  is the axis of rotation for
is the axis of rotation for 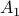 we have
we have 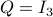 and let
and let 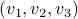 be
be 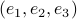 . Then using the procedure from before, we find that
. Then using the procedure from before, we find that 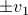 is stable (attracting), while
is stable (attracting), while 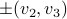 are locally unstable in one direction while
are locally unstable in one direction while 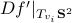 for
for 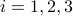 and
and 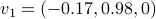 ,
, 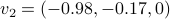 ,
, 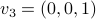 ,
, 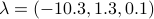 :
: 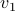 equals that around
equals that around 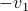 . This explains the attracting great arc parametrized by
. This explains the attracting great arc parametrized by 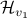 . Note, although the arc is attracting,
. Note, although the arc is attracting, 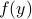 does not vanish on the complete arc, we are locally unstable along
does not vanish on the complete arc, we are locally unstable along 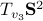 and therefore converge to
and therefore converge to 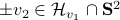 .
.