CDC 2025.

Our paper on Ordering and refining path-complete Lyapunov functions through composition lifts , with Raphael Jungers, will appear at the IEEE CDC 2025 in Rio de Janeiro, Brazil.

In this work, we close Conjecture 8.20, as can be found in the thesis by Debauche. In short, a fruitful approach to study stability of switched systems is to look for multiple Lyapunov functions, this, instead of looking for one possibly highly complicated Lyapunov function. However, in general, we do not yet understand the interplay between the desired stability certificate, the template of the Lyapunov functions (e.g., quadratic forms) and their mutual relationships to accommodate switching. In this work we elaborate on path-complete Lyapunov functions: a graphical framework that aims to elucidate this interplay. Simply put, one can understand Lyapunov inequalities as labeled edges so that arbitrary switching corresponds to graphs containing every possible switching sequence. In turn, this means that we can focus just on the graph structure.

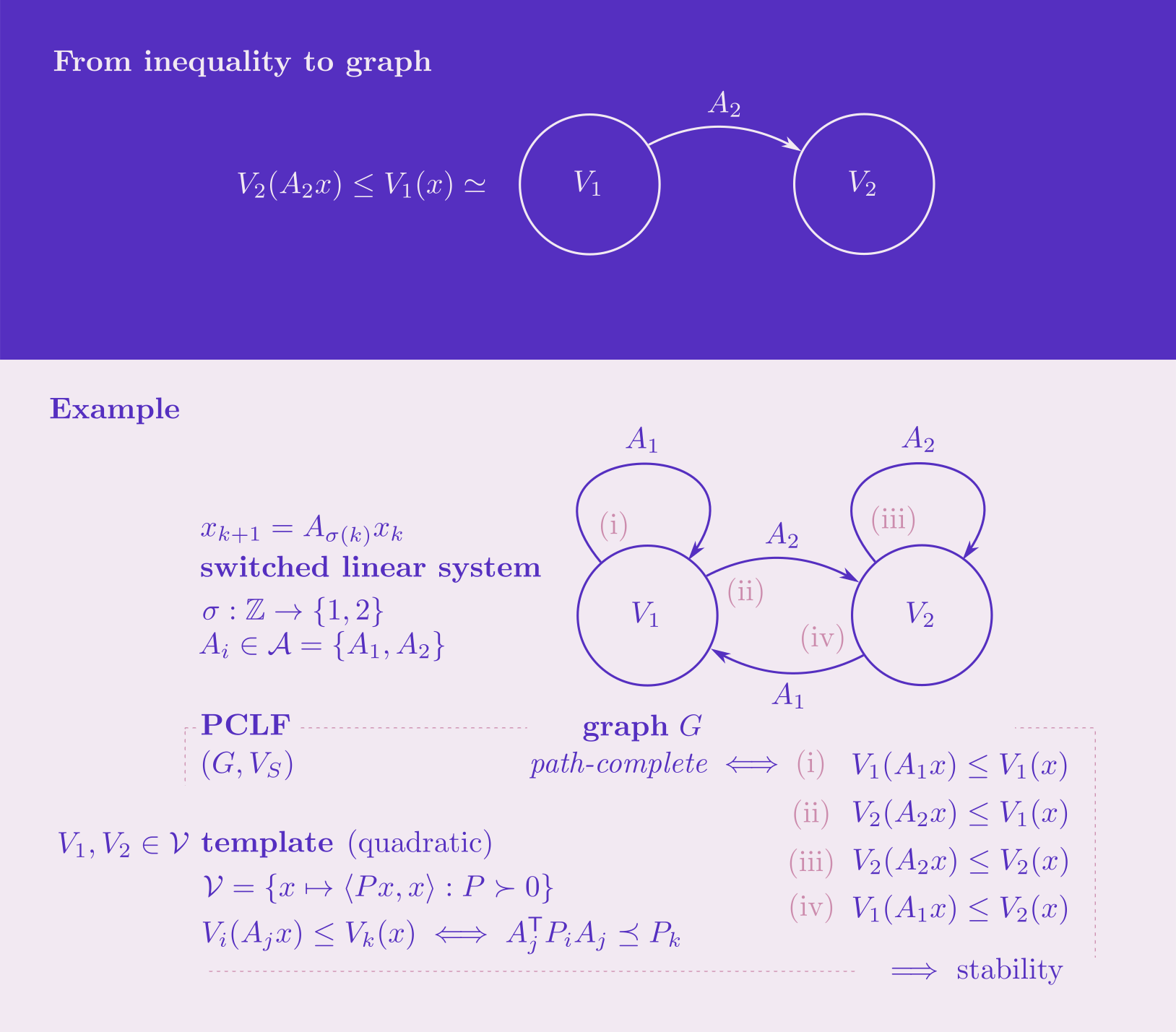
In particular, previously, leveraging the PCLF framework, several preorders were introduced to compare multiple Lyapunov functions. The reason being, although we moved from complicated lists of inequalities to graphs, we can still end up with many different graphs that provide us with stability certificates, what to pick? These preorders are initially algorithmically intractable, essentially due to the algebraic nature of Lyapunov inequalities, yet, lifting techniques were proposed to turn some preorders purely combinatorial and thereby eventually tractable. In this note we show that a conjecture in this area regarding the so-called composition lift, that was believed to be true, is false. This refutal, however, points us to a beneficial structural feature of the composition lift that we exploit to iteratively refine path-complete graphs, plus, it points us to a favourable adaptation of the composition lift.

See you there!