A Peculiar Lower Bound to the Spectral Radius |7 March. 2020|

As a follow up to the previous post, we discuss a lower bound, given as exercise P7.1.14 in (GvL13). I have never seen this bound before, especially not with the corresponding proof, so here we go.

Given any 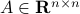$Ain mathbf{R}^{ntimes n}$ , we have the following lower bound:

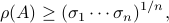
$rho(A)geq (sigma_1cdots sigma_n)^{1/n},$

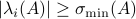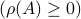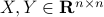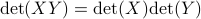which can be thought of as a sharpening of the bound $|lambda_i(A)|geq sigma_{mathrm{min}}(A)$ . In the case of a singular , the bound is trivial (rho(A)geq 0) , but in the general setting it is less obvious. To prove that this holds we need a few ingredients. First, we need that for any $X,Yin mathbf{R}^{ntimes n}$ we have mathrm{det}(XY)=mathrm{det}(X)mathrm{det}(Y) . Then, we construct two decompositions of , (1) the Jordan Normal form 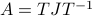$A=TJT^{-1}$ , and (2) the Singular Value Decomposition 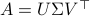$A=USigma V^{top}$ . Using the multiplicative property of the determinant, we find that

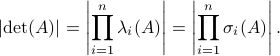
$|mathrm{det}(A)| = left|prod^n_{i=1}lambda_i(A) right| = left| prod^n_{i=1}sigma_i(A) right|.$

Hence, since 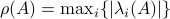$rho(A)=max_i{|lambda_i(A)|}$ it follows that 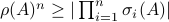$rho(A)^n geq |prod^n_{i=1}sigma_i(A)|$ and thus we have the desired result.

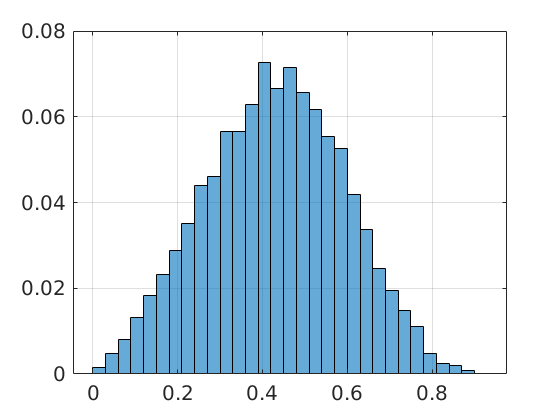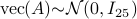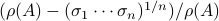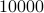(Update 8 March) It is of course interesting to get insight in how sharp this bound is, in general. To that end we consider random matrices $Ain mathbf{R}^{5times 5}$ with $mathrm{vec}(A){sim}mathcal{N}(0,I_{25})$ . When we compute the relative error $(rho(A)-(sigma_1cdots sigma_n)^{1/n})/ rho(A)$ for 10000 samples we obtain the histogram as shown on the left. Clearly, the relative error is not concentrated near 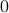. Nevertheless, it is an interesting bound, from a theoretical point of view.

(GvL13) G.H. Golub and C.F. Van Loan: ‘‘Matrix Computations’’, 2013 John Hopkins University Press.