On ‘‘the art of the state’’ |29 December 2022|
tags: math.DS

We owe dynamical systems theory as we know it today largely to Henri Poincaré (1854-1912), whom started this in part being motivated by describing the solar system. Better yet, the goal was to eventually understand its stability. However, we can be a bit more precise regarding what was driving all this work. In the introduction of Les méthodes nouvelles de la mécanique céleste (EN: The new methods of celestial mechanics) - Vol I by Poincaré, published in 1892 (HP92), we find (loosely translated): ‘‘The ultimate goal of Celestial Mechanics is to resolve this great question of whether Newton's law alone explains all astronomical phenomena; the only way to achieve this is to make observations as precise as possible and then compare them with the results of the calculation.’’ and then after a few words on divergent series: ‘‘these developments should attract the attention of geometers, first for the reasons I have just explained and also for the following: the goal of Celestial Mechanics is not reached when one has calculated more or less approximate ephemerides without being able to realize the degree of approximation obtained. If we notice, in fact, a discrepancy between these ephemerides and the observations, we must be able to recognize if Newton's law is at fault or if everything can be explained by the imperfection of the theory.’’ It is perhaps interesting to note that his 1879 thesis entitled: Sur les propriétés des fonctions définies par les équations aux différences partielles (EN: On the properties of functions defined by partial difference equations) was said to lack examples (p.109 FV12).

In the 3 Volumes and well over a 1000 pages of the new celestial mechanics Poincaré develops a host of tools towards the goal sketched above. Indeed, this line of work contributed to the popularizing of the infamous equation

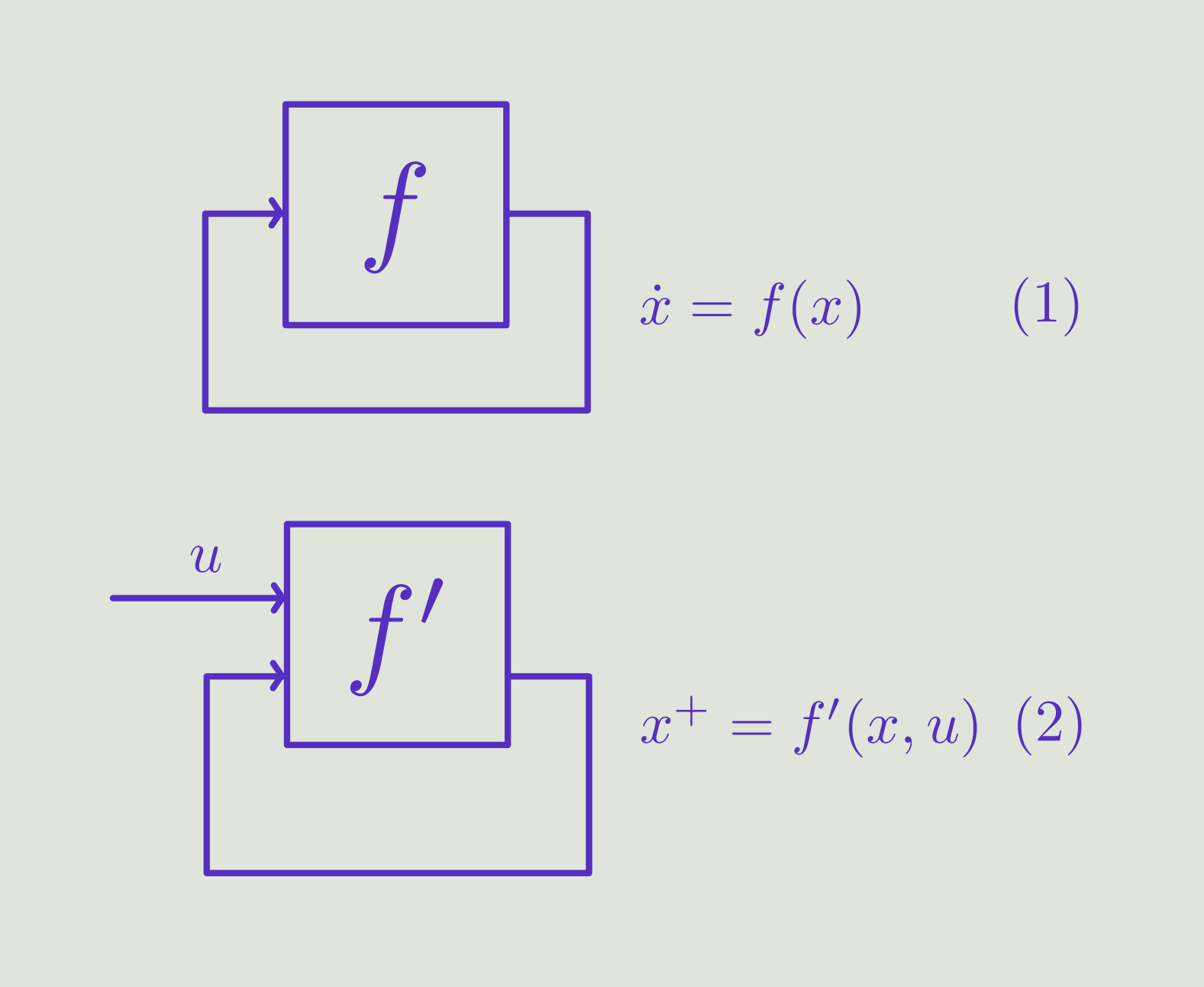
or as used in control theory: , for some ‘‘update’’ operator. However, I would like to argue that the main issue with Equation is not that it is frequently used, but how it is used, moving from the qualitative to the quantitative.

Unfortunately we cannot ask him, but I believe Poincaré would wholeheartedly agree with Sepulchre. Inspired by the beautiful book by Prof. Verhulst (FV12) I will try to briefly illustrate this claim. As put by Verhulst (p.80 FV12): ‘‘In his writings, Poincaré was interested primarily in obtaining insight into physical reality and mathematical reality — two different things.’’ In fact, the relation between analysis and physics was also the subject of Poincaré’s plenary lecture at the first International Congress of Mathematicians, in Zurich (1897). (p.91 FV12).

In what follows we will have a closer look at La Valeur de la Science (EN: The value of science) by Poincaré, published in 1905 (HP05). This is one of his more philosophical works. We already saw how Poincaré was largely motivated by a better understanding of physics. We can further illustrate how he — being one of the founders of many abstract mathematical fields — thought of physics. To that end, consider the following two quotes:

’’when physicists ask of us the solution of a problem, it is not a duty-service they impose upon us, it is on the contrary we who owe them thanks.’’ (p.82 HP05)

‘‘Fourier's series is a precious instrument of which analysis makes continual use, it is by this means that it has been able to represent discontinuous functions; Fourier invented it to solve a problem of physics relative to the propagation of heat. If this problem had not come up naturally, we should never have dared to give discontinuity its rights; we should still long have regarded continuous functions as the only true functions.’’ (p.81 HP05)

What is more, this monograph contains a variety of discussions of the form: ’’If we assume A, B and C, what does this imply?’’ Both mathematically and physically. For instance, after a discussion on Carnot's Theorem (principle) — or if you like the ramifications of a global flow — Poincaré writes the following:

‘‘On this account, if a physical phenomenon is possible, the inverse phenomenon should be equally so, and one should be able to reascend the course of time. Now, it is not so in nature, …’’ (p.96 HP05)

However, Poincaré continues and argues that although notions like friction seem to lead to an irreversible process this is only so because we look at the process through the wrong lens.

‘‘For those who take this point of view, Carnot's principle is only an imperfect principle, a sort of concession to the infirmity of our senses; it is because our eyes are too gross that we do not distinguish the elements of the blend; it is because our hands are too gross that we can not force them to separate; the imaginary demon of Maxwell, who is able to sort the molecules one by one, could well constrain the world to return backward.’’ (p.97 HP05)

Indeed, the section is concluded by stating that perhaps we should look through the lens of statistical mechanics. All to say that if the physical reality is ought the be described, this must be on the basis of solid principles. Let me highlight another principle: conservation of energy. Poincaré writes the following:

‘‘I do not say: Science is useful, because it teaches us to construct machines. I say: Machines are useful, because in working for us, they will some day leave us more time to make science.’’ (p.88 HP05)

‘‘Well, in regard to the universe, the principle of the conservation of energy is able to render us the same service. The universe is also a machine, much more complicated than all those of industry, of which almost all the parts are profoundly hidden from us; but in observing the motion of those that we can see, we are able, by the aid of this principle, to draw conclusions which remain true whatever may be the details of the invisible mechanism which animates them.’’ (p.94 HP05)

Then, a few pages later, his brief story on radium starts as follows:

‘‘At least, the principle of the conservation of energy yet remained to us, and this seemed more solid. Shall I recall to you how it was in its turn thrown into discredit?’’ (p.104 HP05)

Poincaré his viewpoint is to some extent nicely captured by the following piece in the book by Verhulst:

‘‘Consider a mature part of physics, classical mechanics (Poincaré 02). It is of interest that there is a difference in style between British and continental physicists. The former consider mechanics an experimental science, while the physicists in continental Europe formulate classical mechanics as a deductive science based on a priori hypotheses. Poincaré agreed with the English viewpoint, and observed that in the continental books on mechanics, it is never made clear which notions are provided by experience, which by mathematical reasoning, which by conventions and hypotheses.’’ (p.89 FV12)

In fact, for both mathematics and physics Poincaré spoke of conventions, to be understood as a convenience in physics. Overall, we see that Poincaré his attitude to applying mathematical tools to practical problems is significantly more critical than what we see nowadays in some communities. For instance:

‘‘Should we simply deduce all the consequences, and regard them as intangible realities? Far from it; what they should teach us above all is what can and what should be changed.’’ (p.79 HP05)

A clear example of this viewpoint appears in his 1909 lecture series at Göttingen on relativity:

‘‘Let us return to the old mechanics that admitted the principle of relativity. Instead of being founded on experiment, its laws were derived from this fundamental principle. These considerations were satisfactory for purely mechanical phenomena, but the old mechanics didn’t work for important parts of physics, for instance optics.’’ (p.209 FV12)

Now it is tempting to believe that Poincaré would have liked to get rid of ‘‘the old’’, but this is far from the truth.

‘‘We should not have to regret having believed in the principles, and even, since velocities too great for the old formulas would always be only exceptional, the surest way in practise would be still to act as if we continued to believe in them. They are so useful, it would be necessary to keep a place for them. To determine to exclude them altogether would be to deprive oneself of a precious weapon.’’ (p.111 HP05)

The previous was about the ‘‘old’’ and ‘‘new’’ mechanics and how differences in mathematical and physical realities might emerge. Most and for all, the purpose of the above is to show that one of the main figures in abstract dynamical system theory — someone that partially found the field motivated by a computational question — greatly cared about correct modelling.

This is one part of the story. The second part entails the recollection that Poincaré his work was largely qualitative. Precisely this qualitative viewpoint allows for imperfections in the modelling process. However, this also means conclusions can only be qualitative. To provide two examples; based on the Hartman-Grobman theorem and the genericity of hyperbolic equilibrium points it is perfectly reasonable to study linear dynamical systems, however, only to understand local qualitative behaviour of the underlying nonlinear dynamical system. The aim to draw quantitative conclusions is often futile and simply not the purpose of the tools employed. Perhaps more interesting and closer to Poincaré, the Lorenz system, being a simplified mathematical model for atmospheric convection, is well-known for being chaotic. Now, weather-forecasters do use this model, not to predict the weather, but to elucidate why their job is hard!

Summarizing, I believe the editorial note by Prof. Sepulchre is very timely as some have forgotten that the initial dynamical systems work by Poincaré and others was to get a better understanding, to adress questions, to learn from, not to end with. Equation (1) is not magical, but a tool to build the bridge, a tool to see if and where the bridge can be built.