On the complexity of matrix multiplications |10 October 2022|
tags: math.LA
To get some intuition, consider multiplying two complex numbers 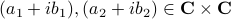 , that is, construct
, that is, construct 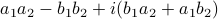 . In this case, the obvious thing to do would lead to 4 multiplications, namely
. In this case, the obvious thing to do would lead to 4 multiplications, namely 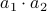 ,
, 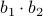 ,
, 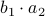 and
and 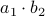 . However, consider using only
. However, consider using only 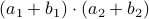 ,
, 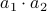 and
and 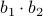 . These multiplications suffice to construct
. These multiplications suffice to construct 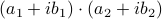 (subtract the latter two from the first one). The emphasis is on multiplications as it seems to be folklore knowledge that multiplications (and especially divisions) are the most costly. However, note that we do use more additive operations. Are these operations not equally ‘‘costly’’? The answer to this question is delicate and still changing!
(subtract the latter two from the first one). The emphasis is on multiplications as it seems to be folklore knowledge that multiplications (and especially divisions) are the most costly. However, note that we do use more additive operations. Are these operations not equally ‘‘costly’’? The answer to this question is delicate and still changing!
When working with integers, additions are indeed generally ‘‘cheaper’’ than multiplications. However, oftentimes we work with floating points. Roughly speaking, these are numbers 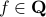 characterized by some (signed) mantissa
characterized by some (signed) mantissa 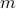 , a base
, a base 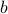 and some (signed) exponent
and some (signed) exponent  , specifically,
, specifically, 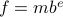 . For instance, consider the addition
. For instance, consider the addition  . To perform the addition, one normalizes the two numbers, e.g., one writes
. To perform the addition, one normalizes the two numbers, e.g., one writes 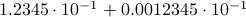 . Then, to perform the addition one needs to take the appropriate precision into account, indeed, the result is
. Then, to perform the addition one needs to take the appropriate precision into account, indeed, the result is 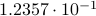 . All this example should convey is that we have sequential steps. Now consider multiplying the same numbers, that is,
. All this example should convey is that we have sequential steps. Now consider multiplying the same numbers, that is, 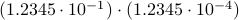 . In this case, one can proceed with two steps in parallel, on the one hand
. In this case, one can proceed with two steps in parallel, on the one hand 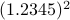 and on the other hand
and on the other hand 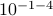 . Again, one needs to take the correct precision into account in the end, but we see that by no means multiplication must be significantly slower in general!
. Again, one needs to take the correct precision into account in the end, but we see that by no means multiplication must be significantly slower in general!
Now back to the matrix multiplication algorithms. Say we have
![A = left[begin{array}{ll} A_{11} & A_{12} A_{21} & A_{22} end{array}right],quad B = left[begin{array}{ll} B_{11} & B_{12} B_{21} & B_{22} end{array}right],](eqs/6805404554309501197-130.png)
then, 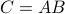 is given by
is given by
![C = left[begin{array}{ll} C_{11} & C_{12} C_{21} & C_{22} end{array}right]= left[begin{array}{ll} A_{11}B_{11}+A_{12}B_{21} & A_{11}B_{12}+A_{12}B_{22} A_{21}B_{11}+A_{22}B_{21} & A_{21}B_{12}+A_{22}B_{22} end{array}right].](eqs/6225513400863626014-130.png)
Indeed, the most straightforward matrix multiplication algorithm for 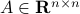 and
and 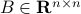 costs you
costs you 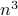 multiplications and
multiplications and 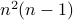 additions.
Using the intuition from the complex multiplication we might expect we can do with fewer multiplications. In 1969 (Numer. Math. 13 354–356) Volker Strassen showed that this is indeed true.
additions.
Using the intuition from the complex multiplication we might expect we can do with fewer multiplications. In 1969 (Numer. Math. 13 354–356) Volker Strassen showed that this is indeed true.
Following his short, but highly influential, paper, let 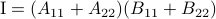 ,
, 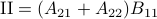 ,
, 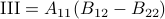 ,
, 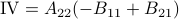 ,
, 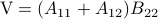 ,
, 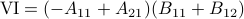 and
and 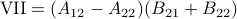 . Then,
. Then, 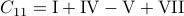 ,
, 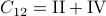 ,
, 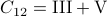 and
and  .
See that we need
.
See that we need 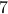 multiplications and
multiplications and 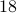 additions to construct
additions to construct 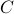 for both
for both  and
and 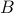 being
being 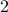 -dimensional. The ‘‘obvious’’ algorithm would cost
-dimensional. The ‘‘obvious’’ algorithm would cost 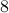 multiplications and
multiplications and 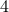 additions. Indeed, one can show now that for matrices of size
additions. Indeed, one can show now that for matrices of size 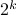 one would need
one would need 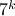 multiplications (via induction). Differently put, one needs
multiplications (via induction). Differently put, one needs 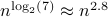 multiplications.
This bound prevails when including all operations, but only asymptotically, in the sense that
multiplications.
This bound prevails when including all operations, but only asymptotically, in the sense that 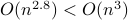 . In practical algorithms, not only multiplications, but also memory and indeed additions play a big role. I am particularly interested how the upcoming DeepMind algorithms will take numerical stability into account.
. In practical algorithms, not only multiplications, but also memory and indeed additions play a big role. I am particularly interested how the upcoming DeepMind algorithms will take numerical stability into account.
*Update: the improved complexity got immediately improved.