Endomorphisms, Tensors in Disguise |18 August 2020|
tags: math.LA
For now, we briefly mention a very beautiful interpretation of 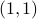 -tensors.
Given some vectorspace
-tensors.
Given some vectorspace  , let
, let 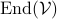 be the set of linear endomorphisms from
be the set of linear endomorphisms from  to
to  .
Indeed, for finite-dimensional vector spaces one can just think of these maps as being parametrized by matrices.
Now, we recall that
.
Indeed, for finite-dimensional vector spaces one can just think of these maps as being parametrized by matrices.
Now, we recall that 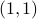 -tensors are multilinear maps which take an element of
-tensors are multilinear maps which take an element of  and its dual space
and its dual space 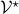 and map it to some real number, that is,
and map it to some real number, that is, 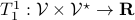 .
.
The claim is that for finite-dimensional  the set
the set 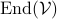 is isomorphic to the set of
is isomorphic to the set of 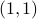 -tensors
-tensors 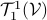 . This is rather intuitive to see, let
. This is rather intuitive to see, let 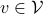 and
and 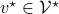 , then, we can write
, then, we can write 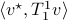 and think of
and think of 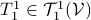 as a matrix. This can be formalized, as is done here by showing there is a bijective map
as a matrix. This can be formalized, as is done here by showing there is a bijective map 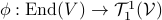 .
So, we can identify any
.
So, we can identify any 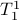 with some
with some 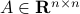 , that is
, that is 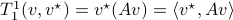 . Similarly, we can fix
. Similarly, we can fix 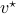 and identify
and identify 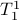 with a linear map in the dual space, that is
with a linear map in the dual space, that is 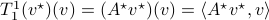 . Regardless, both represent the same tensor evaluation, hence
. Regardless, both represent the same tensor evaluation, hence
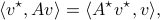
which is indeed the standard dual map definition.
Now we use this relation, recall that discrete-time linear systems are nothing more than maps 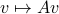 , that is, linear endomorphims, usually on
, that is, linear endomorphims, usually on 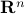 . Using the tensor interpretation we recover what is sometimes called the ‘‘dual system’’ to
. Using the tensor interpretation we recover what is sometimes called the ‘‘dual system’’ to 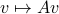 , namely
, namely 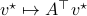 (suggestive notation indeed). Using more traditional notation for the primal:
(suggestive notation indeed). Using more traditional notation for the primal: 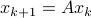 and dual:
and dual: 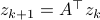 system, we recover that
system, we recover that 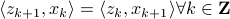 . Then, let
. Then, let 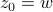 and
and 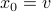 for
for 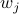 and
and 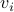 being a left- and right-eigenvector of
being a left- and right-eigenvector of  , respectively. We see that this implies that
, respectively. We see that this implies that 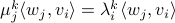 , for
, for 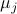 the eigenvalue corresponding to
the eigenvalue corresponding to 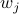 and
and 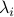 the eigenvalue corresponding to
the eigenvalue corresponding to 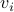 . Hence, in general, the eigenspaces of
. Hence, in general, the eigenspaces of  and
and 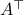 are generically orthogonal.
are generically orthogonal.
In other words, we recover the geometric interpretation of mapping 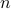 -volumes under
-volumes under  versus
versus 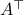 .
.
* See this talk by Daniel.