Almost Surely Investigations in Optimal Control and Dynamical Systems,
Hi, my name is Wout and I am a researcher broadly interested in the mathematical side of systems & control theory.
This page functions as a (web)log of results I find interesting.
Feel free to reach me in case of any hints, tips, tricks, mistakes, ideas or any other comment.
Last summer, I received my PhD in Electrical Engineering from EPFL, working with Daniel Kuhn, as part of the NCCR Automation (a consortium between ETH Zürich, EPFL, EMPA and more). Before moving to Lausanne, I received a MSc in Systems & Control from TU Delft, working with Peyman Mohajerin Esfahani.
During the spring of 2024, I visited KTH Stockholm, the Division of Decision and Control Systems, hosted by Mikael Johansson.
Since August 2024, I joined the Applied Mathematics department (INMA) at UCLouvain, as part of the larger Information and Communication Technologies, Electronics and Applied Mathematics (ICTEAM) institute, working with Raphael Jungers as a postdoctoral fellow.
‘‘He had one big idea and … that was the idea of relating many kinds of mathematical and scientific problems to the study of vector fields on manifolds and the properties of the related flows. That was his central theme and central mechanism.’’ p. 494 Browder on Smale (1993)
 |
Communities |July 02, 2024|
tags: math.OC
As the thesis is printed, it is time to reflect.
Roughly 1 year ago I got the wonderful advice from Roy Smith that whatever you do, you should be part of a community. This stayed with me as four years ago I wrote on my NCCR Automation profile page that “Control problems of the future cannot be solved alone, you need to work together.” and I finally realized — may it be in retrospect — what this really means, I was being kindly welcomed to several communities.
Just last week at the European Control Conference (ECC24), Angela Fontan and Matin Jafarian organized a lunch session on peer review in our community and as Antonella Ferrara emphasized throughout, you engage in the process to contribute to the community, your community. As such, a high quality — and sustainable — conference is intimately connected to the feeling of community. Especially since the conference itself feeds back into our feeling of community (as I am sure you know, everything is just feedback loops..).
ECC24 was a fantastic example when it comes to strengthening that feeling of community and other examples that come to mind are the inControl podcast by Alberto Padoan, Autonomy Talks by Gioele Zardini, the IEEE CSS magazine, the IEEE CSS road map 2030 and recently, the KTH reading group on Control Theory: Twenty-Five Seminal Papers (1932-1981) organized by Miguel Aguiar. The historical components are important not only to better understand our community (the why, how and what), but to always remember we build upon our predecessors, we are part of the same community. Of course, the NCCR Automation contributed enormously and far beyond Switzerland (fellowships, symposia, workshops, …), but even closer to home, ever since the previous century, the Dutch Institute of Systems and Control (DISC) has done a remarkable job bringing and keeping all researchers and students together (MSc programs, a national graduate school, Benelux meetings, …).
The importance of community is sometimes linked to being in need of recognition and to working more effective when in competition. I am sure this is true for some and I am even more sure this is enforced in fields where research is expensive and funding is scarce. Yet, that vast majority of members of the scientific community are not PIs, but students, and for us the community is critically important to create and enforce a sense of belonging. The importance of belonging is widely known — not only in the scientific community — and most of the problems we have here on earth can be directly linked to a lack of belonging and community (as beautifully formulated in Pale Blue Dot by Carl Sagan).
Celebrating personal successes is of great importance, we need our heros, but I want to be part of a scientific community where we focus on progress of the community, what did we solve, what are our open problems, and how do we go about solving them? Looking back, I am happy to see it seems I am part of such a community indeed. Thank you!
Weekend read |May 14, 2023|
tags: math.OC
The ‘‘Control for Societal-scale Challenges: Road Map 2030’’ by the IEEE Control Systems Society (Eds. A. M. Annaswamy, K. H. Johansson, and G. J. Pappas) was published a week ago. This roadmap is a remarkable piece of work, over 250 pages, an outstanding list of authors and coverage of almost anything you can imagine, and more.
If you somehow found your way to this website, then I can only strongly recommend reading this document. Despite many of us being grounded in traditional engineering disciplines, I do agree with the sentiment of this roadmap that the most exciting (future) work is interdisciplinary, this is substantiated by many examples from biology. Better yet, it is stressed that besides familiarizing yourself with the foundations, it is of quintessential importance (and fun I would say) to properly dive into the field where you hope to apply these tools.
‘‘Just because you can formulate and solve an optimization problem does not mean that you have the correct or best cost function.’’ p. 32
Section 4.A on Learning and Data-Driven Control also contains many nice pointers, sometimes alluding to a slight disconnect between practice and theory.
‘‘Sample complexity may only be a coarse measure in this regard, since it is not just the number of samples but the “quality” of the samples that matters.’’ p. 142
The section on safety is also inspiring, just stability will not be enough anymore. However, the most exciting part for me was Chapter 6 on education. The simple goal of making students excited early-on is just great. Also, the aspiration to design the best possible material as a community is more than admirable.
Standing on the shoulders of giants |April 3, 2023|
tags: math.OC
One of the most illuminating activities one can undertake is to go back in time and see how the giants in (y)our field shaped the present. Sadly, several of our giants passed away recently and I want to highlight one of them in particular: Roger W. Brockett.
It is very rare to find elegant and powerful theories in sytems and control that are not related to Brockett somehow, better yet, many powerful theories emerged directly from his work. Let me highlight five topics/directions I find remarkably beautiful:
(Lie algebras): As put by Brockett himself, it is only natural to study the link between Lie theory and control theory since the two are intimately connected through differential equations |1.2|. ‘‘Completing this triangle’’ turned out to be rather fruitful, in particular via Frobenius’ theorem. Brockett played a key role in bringing Lie theoretic methods to control theory, a nice example is his 1973 paper on control systems on spheres (in general, his work on bilinear systems was of great interest) |5|.
(Differential geometric methods): Together with several others, Brockett was one of the first to see how differential geometric methods allowed for elegantly extending ideas from linear control (linear algebra) to the realm of nonlinear control. A key event is the 1972 conference co-organized with David Mayne |1|. See also |2| for a short note on the history of geometric nonlinear control written by Brockett himself.
(Brockett's condition): After pioneering work on (local) nonlinear controllability in the 70s it was observed (by means of low-dimensional counterexamples) that controllability is not sufficient for the existence of a stabilizing continuous feedback. This observation was firmly established in the (1982) 1983 paper by Brockett |3| where he provides his topological necessary condition (Theorem 1 (iii)) for the existence of a stabilizing differentiable feedback, i.e.
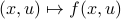 must be locally onto (the same is true for continuous feedback). Formally speaking, this paper is not the first (see Geometrical Methods of Nonlinear Analysis and this paper by Zabczyk), yet, this paper revolutionized how to study necessary conditions for nonlinear stabilization and inspired an incredible amount of work.
must be locally onto (the same is true for continuous feedback). Formally speaking, this paper is not the first (see Geometrical Methods of Nonlinear Analysis and this paper by Zabczyk), yet, this paper revolutionized how to study necessary conditions for nonlinear stabilization and inspired an incredible amount of work.
(Nonlinear control systems): Although we are still far from the definitive control system (modelling) framework, Brockett largely contributed to a better understanding of structure. Evidently, this neatly intertwines with the previous points on bilinear systems (Lie algebras) and differential geometry, however, let me also mention that the fiber bundle perspective (going beyond Cartesian products) is often attributed to Brockett |4|.
(Dynamical systems perspective on optimization): We see nowadays still more and more work on the continuous-time (and system theoretic) viewpoint with respect to optimization algorithms. One can argue that Brockett was also of great importance here. It is not particularly surprising that one can study gradient flows to better understand gradient descent algorithms, however, it turned out that one can understand a fair amount of routines from (numerical) linear algebra through the lens of (continuous-time) dynamical systems. Brockett initiated a significant part of this work with his 1988 paper on the applications of the double bracket equation
![dot{H}=[H,[H,N]]](eqs/229228239358215717-130.png) |6|. For a more complete overview, including a foreword by Brockett, see Optimization and Dynamical Systems.
|6|. For a more complete overview, including a foreword by Brockett, see Optimization and Dynamical Systems.
References (all by Brockett).
|1|: Geometric Methods in System Theory - Proceedings of the NATO Advanced Study Institute held at London, England, August 27-Septernber 7, 1973, ed. with Mayne, D. Reidel Publishing Company (1973).
|1.2|: Chapter: Lie Algebras and Lie groups in Control Theory in |1|.
|2|: The early days of geometric nonlinear control, Automatica (2014).
|3|: Asymptotic stability and feedback stabilization, Differential Geometric Control Theory, ed. with Millman and Sussmann, Birkhäuser (1983).
|4|: Control theory and analytical mechanics, Geometric Control Theory, Lie Groups: History,
Frontiers and Applications, Vol. VII, ed. Martin and Hermann, Math Sci Press, (1976).
|5|: Lie Theory and Control Systems Defined on Spheres, SIAM Journal on Applied Mathematics (1973).
|6|: Dynamical systems that sort lists and solve linear programming problems, IEEE CDC (1988).
See also this 2022 interview (video) with John Baillieul and the foreword to this book for more on the person behind the researcher.
On Critical Transitions in Nature and Society |29 January 2023|
tags: math.DS
The aim of this post is to highlight the 2009 book Critical Transitions in Nature and Society by Prof. Scheffer, which is perhaps more timely than ever and I strongly recommend this book to essentially anyone.
Far too often we (maybe not you) assume that systems are simply reversible, e.g. based on overly simplified models (think of a model corresponding to a flow). The crux of this book is that for many ecosystems such a reversal might be very hard or even practically impossible. Evidently, this observation has many serious ramifications with respect to understanding and tackling climate change.
Mathematically, this can be understood via bifurcation theory, in particular, via folds and cusps, introducing a form of hysteresis. The hysteresis is important here, as this means that simply restoring some parameters of an ecosystem does not directly imply that the state of the ecosystem will return to what these parameters were previously corresponding to.
The book makes a good point that catastrophe- and chaos theory (old friends of bifurcation theory) themselves went through a critical transition, that is, populair media (and some authors) blew-up those theories. To that end, see the following link for a crystal clear introduction to catastrophe theory by Zeeman (including some controversy), as well as this talk by Ralph Abraham on the history (locally) of chaos theory. One might argue that some populair fields these days are also trapped in a similar situation.
Scheffer stays away from drawing overly strong conclusions and throughout the book one can find many discussions on how and if to relate these models to reality. Overall, Scheffer promotes system theoretic thinking. For example, at first sight we might be inclined to link big (stochastic) events, e.g. a meteor hitting the earth, as the cause of some disruptive event, while actually something else might been slowly degrading, e.g. some basin of attraction shrunk, and this stochastic event was just the final push. This makes the book very timely, climate change is slowly changing ecosystems around us, we are just waiting for a detrimental push. To give another example, in Chapter 5 we find an interesting discussion on the relation between biodiversity and stability. Scheffer highlights two points: (i) robustness (there is plently back-up) and (ii) complementation (if many can perform a task, some of them will be very good at it). Overall, the discussions on ‘‘why we have so many animals’’ are very interesting.
One of the main concepts in the book is that of resilience, which is (re)-defined several times (as part of the storyline in the book), in particular, one page 103 we find it being defined as ‘‘the capacity of a system to absorb disturbance and reorganize while undergoing change so as to still retain essentially the same function, structure, identity, and feedbacks.’’ Qualitatively, this is precisely a combination of having an attractor of some system being structurally stable. However, the goal here is to quantify this structural stability to some extent. Indeed, one enters bifurcation theory, or if you like, topological dynamical systems theory.
Throughout, Scheffer provides incredibly many examples of great inspiration to anyone in dynamical system and control theory, e.g. the basin of attraction, multistability and time-separations are recurring themes. My favourite simple example (of positive feedback) being the ice-Albedo feedback, (too) simply put, less ice means less reflection of light and hence more heat absorption, resulting in even less ice (as such, the positive feedback). More details can be found in Chapter 8. Another detailed series of examples is contained in Chapter 7 on shallow lakes. This chapter explains through a qualitative lens why restoring lakes is inherently difficult. Again, (too) simply put, as with ice, if plants disappear in lakes, turbidity is promoted, making it more difficult for plants to return (they need sunlight and thus prefer clear water). For this lake model, one can find some equations in Appendix 12, which is essentially a Lotka-Volterra model. As such, some readers might be unsatisfied when it comes to the mathematical content*. Moreover, at times Scheffer himself describes bifurcations as exotic dynamical systems jargon and throughout the book one might get the feeling that the dynamical systems community has no clue how to handle time-varying models. Luckily, the latter is not completely true. Perhaps the crux here is that we can use more cross-contamination between scientific communities. Especially recognizing these bifurcations (critical transitions), not just in models, but in reality is still a big and pressing open problem.
*A fantastic and easy-going short book on catastrophe theory is written, of course, by Arnold.
The aim of this book was to have a widely accesible mathematical reference. The introduction to this book reads as: ‘‘This booklet explains what catastrophe theory is about and why it arouses such controversy. It also contains non-controversial results from the mathematical theories of singularities and bifurcation.’’
whereas Arnold ends with: ‘‘A qualitative peculiarity of Thom's papers on catastrophe theory is their original style: as one who presenses the direction of future investigations, Thom not only does not have proofs available, but does not even dispose of the precise formulations of his results. Zeeman, an ardent admirer of this style, observes that the meaning of Thom's words becomes clear only after inserting 99 lines of your own between every two of Thom's.’’
Counterexamples 1/N |9 January 2023|
tags: math.An
As nicely felt through the 1964 book Counterexamples in Analysis by Gelbaum and Olmsted, mathematics is not all about proving theorems, equally important is a large collection of (counter)examples to sharpen our understanding of these theorems. This attitude towards mathematics can also be found in books by Arnold, Halmos and many others.
This short post highlights a few of my favourite examples from the book by Gelbaum and Olmsted.
A function that is everywhere finite and everywhere locally unbounded.
A function  is locally bounded when for each point in its domain one can find a neighbourhood
is locally bounded when for each point in its domain one can find a neighbourhood 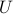 such that
such that  is bounded on
is bounded on 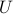 .
Now consider the function
.
Now consider the function 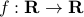 defined by
defined by
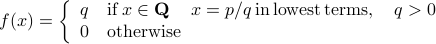
Now assume that we could locally bound  on
on  (some open neighbourhood in
(some open neighbourhood in  ), that means that
), that means that  is bounded on such a neighbourhood and hence, so is
is bounded on such a neighbourhood and hence, so is  .
However, that would imply that
.
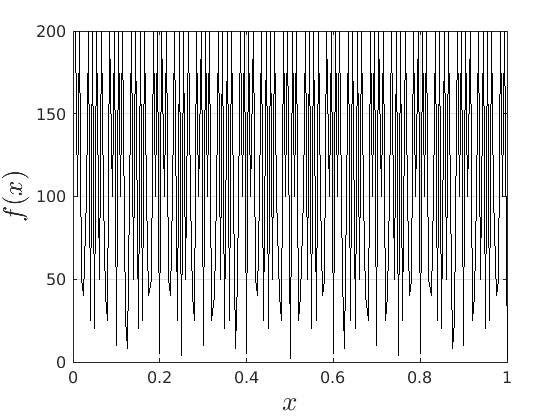
However, that would imply that  only contains finitely many rational numbers! We plot
only contains finitely many rational numbers! We plot  (approximately) below over
(approximately) below over ![[0,1]](eqs/5113014419904972428-130.png) for just
for just 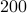 points and observe precisely what one would expect.
points and observe precisely what one would expect.
 |
Two disjoint closed sets that are at a zero distance.
This example is not that surprising, but it nicely illustrates the pitfall of thinking of sets as ‘‘blobs’’ (in Dutch we would say potatoes) in the plane.
Indeed, the counterexample can be interpreted as an asymptotic result.
Consider 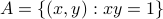 , this set is closed as
, this set is closed as 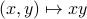 is continuous. Then, take
is continuous. Then, take 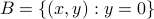 , this set is again closed and clearly
, this set is again closed and clearly  and
and 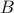 are disjoint. However, since we can write
are disjoint. However, since we can write 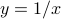 , then as
, then as 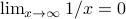 , we find that
, we find that  approaches
approaches 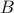 arbitrarily closely. One can create many more examples of this form, e.g., using logarithms.
arbitrarily closely. One can create many more examples of this form, e.g., using logarithms.
An open and closed metric ball with the same center and radius such that the closure of the open ball is unequal to the closed ball.
This last example is again not that surprising if you are used to go beyond Euclidean spaces. Let 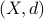 be a metric space under the metric
be a metric space under the metric
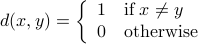
Now assume that  is not simply a singleton. Then, let
is not simply a singleton. Then, let 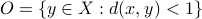 be the open metric ball of radius
be the open metric ball of radius  centered at
centered at 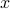 and similarly, let
and similarly, let 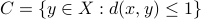 be the closed metric ball of radius
be the closed metric ball of radius  centered at
centered at 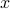 . Indeed,
. Indeed, 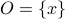 whereas
whereas  . Now to construct the closure of
. Now to construct the closure of 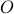 , we must first understand the topology induced by the metric
, we must first understand the topology induced by the metric 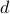 . In other words, we must understand the limit points of
. In other words, we must understand the limit points of 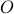 . Indeed,
. Indeed, 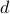 is the discrete metric and this metric induces the discrete topology on
is the discrete metric and this metric induces the discrete topology on  . Hence, it follows — which is perhaps the counterintuitive part, that
. Hence, it follows — which is perhaps the counterintuitive part, that 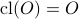 and hence
and hence 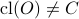 . This example also nicely shows a difference between metrics and norms. As norms satisfy
. This example also nicely shows a difference between metrics and norms. As norms satisfy 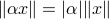 (absolute homogeneity) one cannot have the discontinuous behaviour from the example above.
(absolute homogeneity) one cannot have the discontinuous behaviour from the example above.
Further examples I particularly enjoyed are a discontinuous linear function, a function that is discontinuous in two variables, yet continuous in both variables separately and all examples related to Cantor. This post is inspired by TAing for Analysis 1 and will be continued in the near future.
On ‘‘the art of the state’’ |29 December 2022|
tags: math.DS
In the last issue of the IEEE Control Systems Magazine, Prof. Sepulchre wrote an exhilarating short piece on the art of the state, or as he (also) puts it ‘‘the definite victory of computation over modeling in science and engineering’’. As someone with virtually no track record, I am happy to also shed my light on the matter.
We owe dynamical systems theory as we know it today largely to Henri Poincaré (1854-1912), whom started this in part being motivated by describing the solar system. Better yet, the goal was to eventually understand its stability. However, we can be a bit more precise regarding what was driving all this work. In the introduction of Les méthodes nouvelles de la mécanique céleste (EN: The new methods of celestial mechanics) - Vol I by Poincaré, published in 1892 (HP92), we find (loosely translated): ‘‘The ultimate goal of Celestial Mechanics is to resolve this great question of whether Newton's law alone explains all astronomical phenomena; the only way to achieve this is to make observations as precise as possible and then compare them with the results of the calculation.’’ and then after a few words on divergent series: ‘‘these developments should attract the attention of geometers, first for the reasons I have just explained and also for the following: the goal of Celestial Mechanics is not reached when one has calculated more or less approximate ephemerides without being able to realize the degree of approximation obtained. If we notice, in fact, a discrepancy between these ephemerides and the observations, we must be able to recognize if Newton's law is at fault or if everything can be explained by the imperfection of the theory.’’ It is perhaps interesting to note that his 1879 thesis entitled: Sur les propriétés des fonctions définies par les équations aux différences partielles (EN: On the properties of functions defined by partial difference equations) was said to lack examples (p.109 FV12).
In the 3 Volumes and well over a 1000 pages of the new celestial mechanics Poincaré develops a host of tools towards the goal sketched above. Indeed, this line of work contributed to the popularizing of the infamous equation
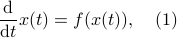
or as used in control theory: 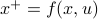 , for
, for 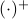 some ‘‘update’’ operator. However, I would like to argue that the main issue with Equation
some ‘‘update’’ operator. However, I would like to argue that the main issue with Equation  is not that it is frequently used, but how it is used, moving from the qualitative to the quantitative.
is not that it is frequently used, but how it is used, moving from the qualitative to the quantitative.
Unfortunately we cannot ask him, but I believe Poincaré would wholeheartedly agree with Sepulchre. Inspired by the beautiful book by Prof. Verhulst (FV12) I will try to briefly illustrate this claim. As put by Verhulst (p.80 FV12): ‘‘In his writings, Poincaré was interested primarily in obtaining insight into physical reality and mathematical reality — two different things.’’ In fact, the relation between analysis and physics was also the subject of Poincaré’s plenary lecture at the first International Congress of Mathematicians, in Zurich (1897). (p.91 FV12).
In what follows we will have a closer look at La Valeur de la Science (EN: The value of science) by Poincaré, published in 1905 (HP05). This is one of his more philosophical works. We already saw how Poincaré was largely motivated by a better understanding of physics. We can further illustrate how he — being one of the founders of many abstract mathematical fields — thought of physics. To that end, consider the following two quotes:
’’when physicists ask of us the solution of a problem, it is not a duty-service they impose upon us, it is on the contrary we who owe them thanks.’’ (p.82 HP05)
‘‘Fourier's series is a precious instrument of which analysis makes continual use, it is by this means that it has been able to represent discontinuous functions; Fourier invented it to solve a problem of physics relative to the propagation of heat. If this problem had not come up naturally, we should never have dared to give discontinuity its rights; we should still long have regarded continuous functions as the only true functions.’’ (p.81 HP05)
What is more, this monograph contains a variety of discussions of the form: ’’If we assume A, B and C, what does this imply?’’ Both mathematically and physically. For instance, after a discussion on Carnot's Theorem (principle) — or if you like the ramifications of a global flow — Poincaré writes the following:
‘‘On this account, if a physical phenomenon is possible, the inverse phenomenon should be equally so, and one should be able to reascend the course of time. Now, it is not so in nature, …’’ (p.96 HP05)
However, Poincaré continues and argues that although notions like friction seem to lead to an irreversible process this is only so because we look at the process through the wrong lens.
‘‘For those who take this point of view, Carnot's principle is only an imperfect principle, a sort of concession to the infirmity of our senses; it is because our eyes are too gross that we do not distinguish the elements of the blend; it is because our hands are too gross that we can not force them to separate; the imaginary demon of Maxwell, who is able to sort the molecules one by one, could well constrain the world to return backward.’’ (p.97 HP05)
Indeed, the section is concluded by stating that perhaps we should look through the lens of statistical mechanics. All to say that if the physical reality is ought the be described, this must be on the basis of solid principles. Let me highlight another principle: conservation of energy. Poincaré writes the following:
‘‘I do not say: Science is useful, because it teaches us to construct machines. I say: Machines are useful, because in working for us, they will some day leave us more time to make science.’’ (p.88 HP05)
‘‘Well, in regard to the universe, the principle of the conservation of energy is able to render us the same service. The universe is also a machine, much more complicated than all those of industry, of which almost all the parts are profoundly hidden from us; but in observing the motion of those that we can see, we are able, by the aid of this principle, to draw conclusions which remain true whatever may be the details of the invisible mechanism which animates them.’’ (p.94 HP05)
Then, a few pages later, his brief story on radium starts as follows:
‘‘At least, the principle of the conservation of energy yet remained to us, and this seemed more solid. Shall I recall to you how it was in its turn thrown into discredit?’’ (p.104 HP05)
Poincaré his viewpoint is to some extent nicely captured by the following piece in the book by Verhulst:
‘‘Consider a mature part of physics, classical mechanics (Poincaré 02). It is of interest that there is a difference in style between British and continental physicists. The former consider mechanics an experimental science, while the physicists in continental Europe formulate classical mechanics as a deductive science based on a priori hypotheses. Poincaré agreed with the English viewpoint, and observed that in the continental books on mechanics, it is never made clear which notions are provided by experience, which by mathematical reasoning, which by conventions and hypotheses.’’ (p.89 FV12)
In fact, for both mathematics and physics Poincaré spoke of conventions, to be understood as a convenience in physics. Overall, we see that Poincaré his attitude to applying mathematical tools to practical problems is significantly more critical than what we see nowadays in some communities. For instance:
‘‘Should we simply deduce all the consequences, and regard them as intangible realities? Far from it; what they should teach us above all is what can and what should be changed.’’ (p.79 HP05)
A clear example of this viewpoint appears in his 1909 lecture series at Göttingen on relativity:
‘‘Let us return to the old mechanics that admitted the principle of relativity. Instead of being founded on experiment, its laws were derived from this fundamental principle. These considerations were satisfactory for purely mechanical phenomena, but the old mechanics didn’t work for important parts of physics, for instance optics.’’ (p.209 FV12)
Now it is tempting to believe that Poincaré would have liked to get rid of ‘‘the old’’, but this is far from the truth.
‘‘We should not have to regret having believed in the principles, and even, since velocities too great for the old formulas would always be only exceptional, the surest way in practise would be still to act as if we continued to believe in them. They are so useful, it would be necessary to keep a place for them. To determine to exclude them altogether would be to deprive oneself of a precious weapon.’’ (p.111 HP05)
The previous was about the ‘‘old’’ and ‘‘new’’ mechanics and how differences in mathematical and physical realities might emerge. Most and for all, the purpose of the above is to show that one of the main figures in abstract dynamical system theory — someone that partially found the field motivated by a computational question — greatly cared about correct modelling.
This is one part of the story. The second part entails the recollection that Poincaré his work was largely qualitative. Precisely this qualitative viewpoint allows for imperfections in the modelling process. However, this also means conclusions can only be qualitative. To provide two examples; based on the Hartman-Grobman theorem and the genericity of hyperbolic equilibrium points it is perfectly reasonable to study linear dynamical systems, however, only to understand local qualitative behaviour of the underlying nonlinear dynamical system. The aim to draw quantitative conclusions is often futile and simply not the purpose of the tools employed. Perhaps more interesting and closer to Poincaré, the Lorenz system, being a simplified mathematical model for atmospheric convection, is well-known for being chaotic. Now, weather-forecasters do use this model, not to predict the weather, but to elucidate why their job is hard!
Summarizing, I believe the editorial note by Prof. Sepulchre is very timely as some have forgotten that the initial dynamical systems work by Poincaré and others was to get a better understanding, to adress questions, to learn from, not to end with. Equation (1) is not magical, but a tool to build the bridge, a tool to see if and where the bridge can be built.
On the complexity of matrix multiplications |10 October 2022|
tags: math.LA
Recently, DeepMind published new work on ‘‘discovering’’ numerical linear algebra routines. This is remarkable, but I leave the assesment of this contribution to others. Rather, I like to highlight the earlier discovery of Strassen. Namely, how to improve upon the obvious matrix multiplication algorithm.
To get some intuition, consider multiplying two complex numbers 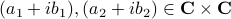 , that is, construct
, that is, construct 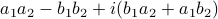 . In this case, the obvious thing to do would lead to 4 multiplications, namely
. In this case, the obvious thing to do would lead to 4 multiplications, namely 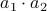 ,
, 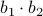 ,
, 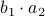 and
and 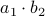 . However, consider using only
. However, consider using only 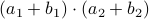 ,
, 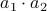 and
and 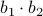 . These multiplications suffice to construct
. These multiplications suffice to construct 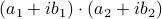 (subtract the latter two from the first one). The emphasis is on multiplications as it seems to be folklore knowledge that multiplications (and especially divisions) are the most costly. However, note that we do use more additive operations. Are these operations not equally ‘‘costly’’? The answer to this question is delicate and still changing!
(subtract the latter two from the first one). The emphasis is on multiplications as it seems to be folklore knowledge that multiplications (and especially divisions) are the most costly. However, note that we do use more additive operations. Are these operations not equally ‘‘costly’’? The answer to this question is delicate and still changing!
When working with integers, additions are indeed generally ‘‘cheaper’’ than multiplications. However, oftentimes we work with floating points. Roughly speaking, these are numbers  characterized by some (signed) mantissa
characterized by some (signed) mantissa  , a base
, a base 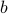 and some (signed) exponent
and some (signed) exponent  , specifically,
, specifically, 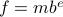 . For instance, consider the addition
. For instance, consider the addition  . To perform the addition, one normalizes the two numbers, e.g., one writes
. To perform the addition, one normalizes the two numbers, e.g., one writes 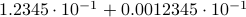 . Then, to perform the addition one needs to take the appropriate precision into account, indeed, the result is
. Then, to perform the addition one needs to take the appropriate precision into account, indeed, the result is 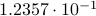 . All this example should convey is that we have sequential steps. Now consider multiplying the same numbers, that is,
. All this example should convey is that we have sequential steps. Now consider multiplying the same numbers, that is, 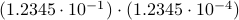 . In this case, one can proceed with two steps in parallel, on the one hand
. In this case, one can proceed with two steps in parallel, on the one hand 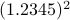 and on the other hand
and on the other hand 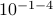 . Again, one needs to take the correct precision into account in the end, but we see that by no means multiplication must be significantly slower in general!
. Again, one needs to take the correct precision into account in the end, but we see that by no means multiplication must be significantly slower in general!
Now back to the matrix multiplication algorithms. Say we have
![A = left[begin{array}{ll} A_{11} & A_{12} A_{21} & A_{22} end{array}right],quad B = left[begin{array}{ll} B_{11} & B_{12} B_{21} & B_{22} end{array}right],](eqs/6805404554309501197-130.png)
then, 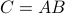 is given by
is given by
![C = left[begin{array}{ll} C_{11} & C_{12} C_{21} & C_{22} end{array}right]= left[begin{array}{ll} A_{11}B_{11}+A_{12}B_{21} & A_{11}B_{12}+A_{12}B_{22} A_{21}B_{11}+A_{22}B_{21} & A_{21}B_{12}+A_{22}B_{22} end{array}right].](eqs/6225513400863626014-130.png)
Indeed, the most straightforward matrix multiplication algorithm for 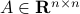 and
and 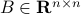 costs you
costs you 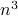 multiplications and
multiplications and 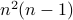 additions.
Using the intuition from the complex multiplication we might expect we can do with fewer multiplications. In 1969 (Numer. Math. 13 354–356) Volker Strassen showed that this is indeed true.
additions.
Using the intuition from the complex multiplication we might expect we can do with fewer multiplications. In 1969 (Numer. Math. 13 354–356) Volker Strassen showed that this is indeed true.
Following his short, but highly influential, paper, let 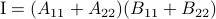 ,
, 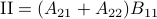 ,
, 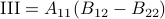 ,
, 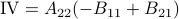 ,
, 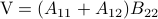 ,
, 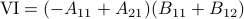 and
and 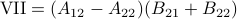 . Then,
. Then, 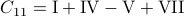 ,
, 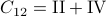 ,
, 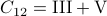 and
and  .
See that we need
.
See that we need 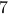 multiplications and
multiplications and 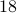 additions to construct
additions to construct 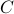 for both
for both  and
and 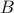 being
being  -dimensional. The ‘‘obvious’’ algorithm would cost
-dimensional. The ‘‘obvious’’ algorithm would cost 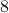 multiplications and
multiplications and 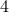 additions. Indeed, one can show now that for matrices of size
additions. Indeed, one can show now that for matrices of size 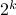 one would need
one would need 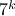 multiplications (via induction). Differently put, one needs
multiplications (via induction). Differently put, one needs 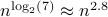 multiplications.
This bound prevails when including all operations, but only asymptotically, in the sense that
multiplications.
This bound prevails when including all operations, but only asymptotically, in the sense that 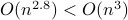 . In practical algorithms, not only multiplications, but also memory and indeed additions play a big role. I am particularly interested how the upcoming DeepMind algorithms will take numerical stability into account.
. In practical algorithms, not only multiplications, but also memory and indeed additions play a big role. I am particularly interested how the upcoming DeepMind algorithms will take numerical stability into account.
*Update: the improved complexity got immediately improved.
A corollary |6 June 2022|
tags: math.DS
The lack of mathematically oriented people in the government is an often observed phenomenon |1|. In this short note we clarify that this is a corollary to ‘‘An application of Poincare's recurrence theorem to adademic adminstration’’, by Kenneth R. Meyer. In particular, since the governmental system is qualitatively the same as that of academic administration, it is also conservative. However - due to well-known results also pioneered by Poincare - this implies the following.
Corollary: The government is non-exact.
Co-observability |6 January 2022|
tags: math.OC
A while ago Prof. Jan H. van Schuppen published his book Control and System Theory of Discrete-Time Stochastic Systems. In this post I would like to highlight one particular concept from the book: (stochastic) co-observability, which is otherwise rarely discussed.
We start with recalling observability. Given a linear-time-invariant system with 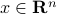 ,
, 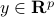 :
:
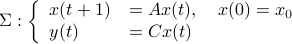
one might wonder if the initial state 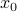 can be recovered from a sequence of outputs
can be recovered from a sequence of outputs  . (This is of great use in feedback problems.) By observing that
. (This is of great use in feedback problems.) By observing that 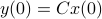 ,
, 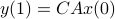 ,
, 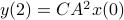 one is drawn to the observability matrix
one is drawn to the observability matrix
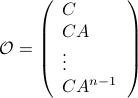
Without going into detectability, when 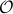 is full-rank, one can (uniquely) recover
is full-rank, one can (uniquely) recover 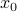 (proof by contradiction). If this is the case, we say that
(proof by contradiction). If this is the case, we say that 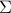 , or equivalenty the pair
, or equivalenty the pair 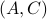 , is observable. Note that using a larger matrix (more data) is redudant by the Cayley-Hamilton theorem (If
, is observable. Note that using a larger matrix (more data) is redudant by the Cayley-Hamilton theorem (If 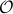 would not be full-rank, but by adding
would not be full-rank, but by adding 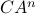 “from below” it would somehow be full-rank, one would contradict the Cayley-Hamilton theorem.).
Also note that in practice one does not “invert”
“from below” it would somehow be full-rank, one would contradict the Cayley-Hamilton theorem.).
Also note that in practice one does not “invert” 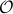 but rather uses a (Luenberger) observer (or a Kalman filter).
but rather uses a (Luenberger) observer (or a Kalman filter).
Now lets continue with a stochastic (Gaussian) system, can we do something similar? Here it will be even more important to only think about observability matrices as merely tools to assert observability. Let 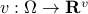 be a zero-mean Gaussian random variable with covariance
be a zero-mean Gaussian random variable with covariance 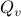 and define for some matrices
and define for some matrices 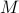 and
and  the stochastic system
the stochastic system
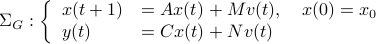
We will assume that  is asymptotically (exponentially stable) such that the Lyapunov equation describing the (invariant) state-covariance is defined:
is asymptotically (exponentially stable) such that the Lyapunov equation describing the (invariant) state-covariance is defined:
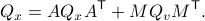
Now the support of the state 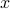 is the range of
is the range of 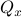 .
.
A convenient tool to analyze 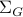 will be the characteristic function of a Gaussian random variable
will be the characteristic function of a Gaussian random variable  , defined as
, defined as ![varphi(omega)=mathbf{E}[mathrm{exp}(ilangle omega, Xrangle)]](eqs/1509536698066778096-130.png) .
It can be shown that for a Gaussian random variable
.
It can be shown that for a Gaussian random variable 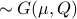
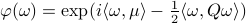 .
With this notation fixed, we say that
.
With this notation fixed, we say that 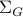 is stochastically observable on the internal
is stochastically observable on the internal 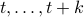 if the map
if the map
![x(t)mapsto mathbf{E}[mathrm{exp}(ilangle omega,bar{y}rangle|mathcal{F}^{x(t)}],quad bar{y}=(y(t),dots,y(t+k))in mathbf{R}^{pcdot(k+1)}quad forall omega](eqs/853891715523836887-130.png)
is injective on the support of 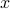 (note the
(note the 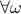 ). The intuition is the same as before, but now we want the state to give rise to an unique (conditional) distribution. At this point is seems rather complicated, but as it turns out, the conditions will be similar to ones from before. We start by writing down explicit expressions for
). The intuition is the same as before, but now we want the state to give rise to an unique (conditional) distribution. At this point is seems rather complicated, but as it turns out, the conditions will be similar to ones from before. We start by writing down explicit expressions for 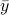 , as
, as
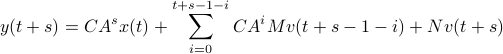
we find that
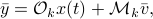
for 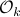 the observability matrix corresponding to the data (length) of
the observability matrix corresponding to the data (length) of 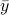 ,
, 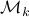 a matrix containing all the noise related terms and
a matrix containing all the noise related terms and 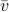 a stacked vector of noises similar to
a stacked vector of noises similar to 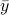 . It follows that
. It follows that ![x(t)mapsto mathbf{E}[mathrm{exp}(ilangle omega,bar{y})|mathcal{F}^{x(t)}]](eqs/1452358234763943133-130.png) is given by
is given by 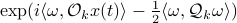 , for
, for ![mathcal{Q}_k = mathbf{E}[mathcal{M}_kbar{v}bar{v}^{mathsf{T}}mathcal{M}_k^{mathsf{T}}]](eqs/8712945555052273745-130.png) . Injectivity of this map clearly relates directly to injectivity of
. Injectivity of this map clearly relates directly to injectivity of 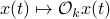 . As such (taking the support into account), a neat characterization of stochastic observability is that
. As such (taking the support into account), a neat characterization of stochastic observability is that 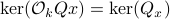 .
.
Then, to introduce the notion of stochastic co-observability we need to introduce the backward representation of a system. We term system representations like  and
and 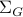 “forward” representations as
“forward” representations as 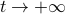 . Assume that
. Assume that 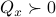 , then see that the forward representation of a system matrix, denoted
, then see that the forward representation of a system matrix, denoted 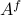 is given by
is given by ![A^f = mathbf{E}[x(t+1)x(t)^{mathsf{T}}]Q_x^{-1}](eqs/3247376240463532393-130.png) . In a similar vein, the backward representation is given by
. In a similar vein, the backward representation is given by ![A^b=mathbf{E}[x(t-1)x(t)^{mathsf{T}}]Q_x^{-1}](eqs/3587697042984921977-130.png) .
Doing the same for the output matrix
.
Doing the same for the output matrix 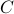 yields
yields ![C^b=mathbf{E}[y(t-1)x(t)^{mathsf{T}}]Q_x^{-1}](eqs/2184503885116254462-130.png) and thereby the complete backward system
and thereby the complete backward system
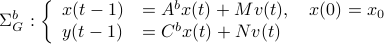
Note, to keep 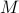 and
and  fixed, we adjust the distribution of
fixed, we adjust the distribution of  .
Indeed, when
.
Indeed, when 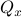 is not full-rank, the translation between forward and backward representations is not well-defined. Initial conditions
is not full-rank, the translation between forward and backward representations is not well-defined. Initial conditions 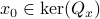 cannot be recovered.
cannot be recovered.
To introduce co-observability, ignore the noise for the moment and observe that 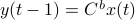 ,
, 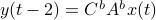 , and so forth.
We see that when looking at observability using the backward representation, we can ask if it possible to recover the current state using past outputs. Standard observability looks at past states instead. With this in mind we can define stochastic co-observability on the interval
, and so forth.
We see that when looking at observability using the backward representation, we can ask if it possible to recover the current state using past outputs. Standard observability looks at past states instead. With this in mind we can define stochastic co-observability on the interval 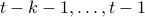 be demanding that the map
be demanding that the map
![x(t)mapsto mathbf{E}[mathrm{exp}(ilangle omega,bar{y}^brangle|mathcal{F}^{x(t)}],quad bar{y}^b=(y(t-1),dots,y(t-k-1))in mathbf{R}^{pcdot(k+1)}quad forall omega](eqs/2807210638750947645-130.png)
is injective on the support of 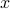 (note the
(note the 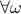 ). Of course, one needs to make sure that
). Of course, one needs to make sure that 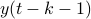 is defined. It is no surprise that the conditions for stochastic co-observability will also be similar, but now using the co-observability matrix. What is however remarkable, is that these notions do not always coincide.
is defined. It is no surprise that the conditions for stochastic co-observability will also be similar, but now using the co-observability matrix. What is however remarkable, is that these notions do not always coincide.
Lets look at when this can happen and what this implies. One reason to study these kind of questions is to say something about (minimal) realizations of stochastic processes. Simply put, what is the smallest (as measured by the dimension of the state 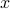 ) system
) system 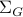 that gives rise to a certain output process. When observability and co-observability do not agree, this indicates that the representation is not minimal. To get some intuition, we can do an example as adapted from the book. Consider the scalar (forward) Gaussian system
that gives rise to a certain output process. When observability and co-observability do not agree, this indicates that the representation is not minimal. To get some intuition, we can do an example as adapted from the book. Consider the scalar (forward) Gaussian system
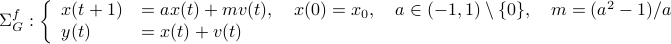
for 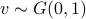 . The system is stochastically observable as
. The system is stochastically observable as 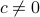 and
and 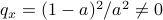 . Now for stochastic co-observability we see that
. Now for stochastic co-observability we see that ![c^b=mathbf{E}[y(t-1)x(t)]q_x^{-1}]=0](eqs/6755659394537019237-130.png) , as such the system is not co-observable. What this shows is that
, as such the system is not co-observable. What this shows is that 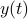 behaves as a Gaussian random variable, no internal dynamics are at play and such a minimal realization is of dimension
behaves as a Gaussian random variable, no internal dynamics are at play and such a minimal realization is of dimension 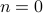 .
.
For this and a lot more, have a look at the book!
Fair convex partitioning |26 September 2021|
tags: math.OC
When learning about convex sets, the definitions seem so clean that perhaps you think all is known what could be known about finite-dimensional convex geometry. In this short note we will look at a problem which is still largely open beyond the planar case. This problem is called the fair partitioning problem.
In the  -dimensional case, the question is the following, given any integer
-dimensional case, the question is the following, given any integer 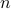 , can a convex set
, can a convex set 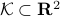 be divided into
be divided into 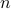 convex sets all of equal area and perimeter.
Differently put, does there exist a fair convex partitioning, see Figure 1.
convex sets all of equal area and perimeter.
Differently put, does there exist a fair convex partitioning, see Figure 1.
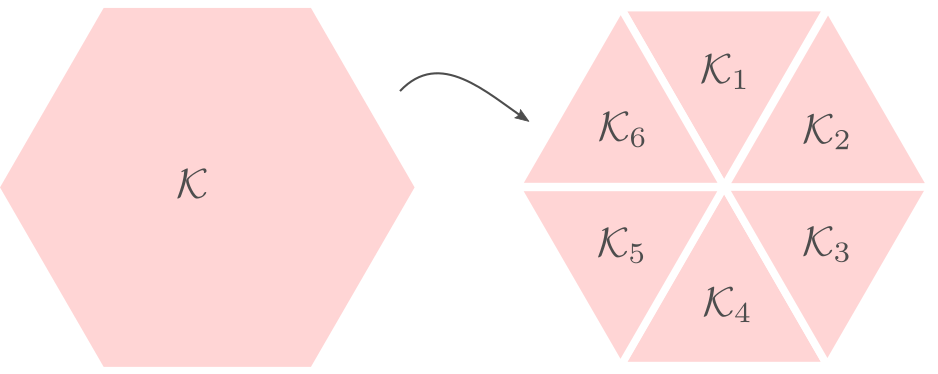 |
Figure 1:
A partition of |
This problem was affirmatively solved in 2018, see this paper.
As you can see, this work was updated just a few months ago. The general proof is involved, lets see if we can do the case for a compact set and 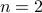 .
.
First of all, when splitting  (into just two sets) you might think of many different methods to do so. What happens when the line is curved? The answer is that when the line is curved, one of the resulting sets must be non-convex, compare the options in Figure 2.
(into just two sets) you might think of many different methods to do so. What happens when the line is curved? The answer is that when the line is curved, one of the resulting sets must be non-convex, compare the options in Figure 2.
 |
Figure 2:
A partitioning of the square in |
This observation is particularly useful as it implies we only need to look at two points on the boundary of  (and the line between them). As
(and the line between them). As  is compact we can always select a cut such that the resulting perimeters of
is compact we can always select a cut such that the resulting perimeters of 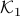 and
and 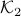 are equal.
are equal.
Let us assume that the points  and
and 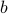 in Figure 3.(i) are like that. If we start moving them around with equal speed, the resulting perimeters remain fixed. Better yet, as the cut is a straight-line, the volumes (area) of the resulting set
in Figure 3.(i) are like that. If we start moving them around with equal speed, the resulting perimeters remain fixed. Better yet, as the cut is a straight-line, the volumes (area) of the resulting set 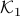 and
and 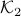 change continuously. Now the result follows from the Intermediate Value Theorem and seeing that we can flip the meaning of
change continuously. Now the result follows from the Intermediate Value Theorem and seeing that we can flip the meaning of 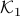 and
and 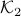 , see Figure 3.(iii).
, see Figure 3.(iii).
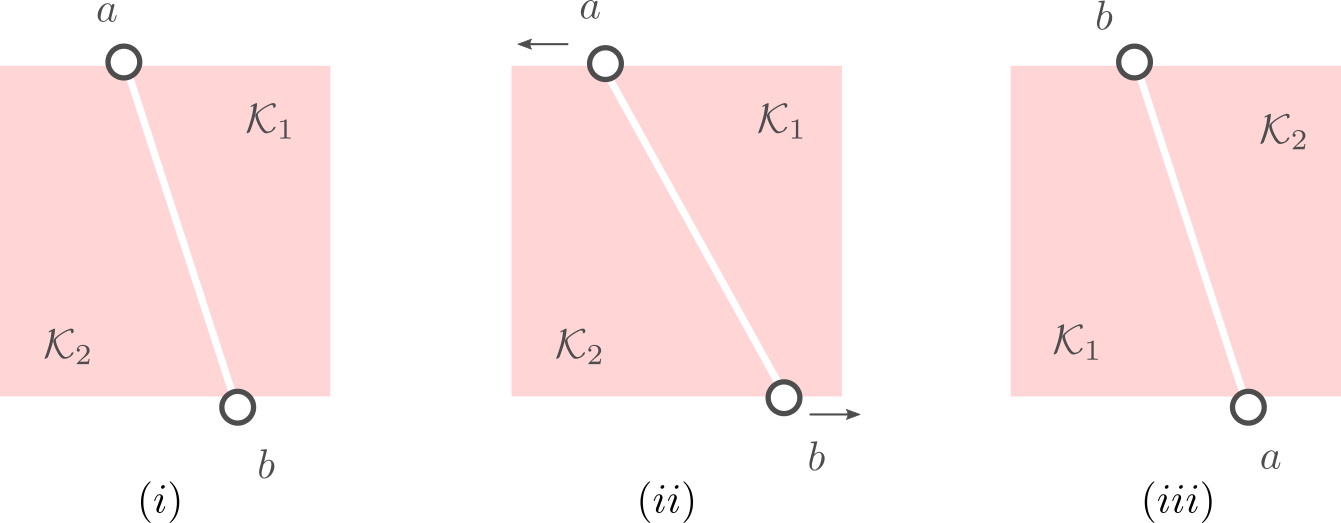 |
Figure 3:
By moving the points |
Solving Linear Programs via Isospectral flows |05 September 2021|
tags: math.OC, math.DS, math.DG
In this post we will look at one of the many remarkable findings by Roger W. Brockett. Consider a Linear Program (LP)
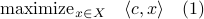
parametrized by the compact set 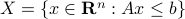 and a suitable triple
and a suitable triple 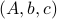 .
As a solution to
.
As a solution to  can always be found to be a vertex of
can always be found to be a vertex of  , a smooth method to solve
, a smooth method to solve  seems somewhat awkward.
We will see that one can construct a so-called isospectral flow that does the job.
Here we will follow Dynamical systems that sort lists, diagonalize matrices and solve linear programming problems, by Roger. W. Brockett (CDC 1988) and the book Optimization and Dynamical Systems edited by Uwe Helmke and John B. Moore (Springer 2ed. 1996).
Let
seems somewhat awkward.
We will see that one can construct a so-called isospectral flow that does the job.
Here we will follow Dynamical systems that sort lists, diagonalize matrices and solve linear programming problems, by Roger. W. Brockett (CDC 1988) and the book Optimization and Dynamical Systems edited by Uwe Helmke and John B. Moore (Springer 2ed. 1996).
Let  have
have 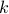 vertices, then one can always find a map
vertices, then one can always find a map 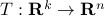 , mapping the simplex
, mapping the simplex 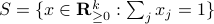 onto
onto  .
Indeed, with some abuse of notation, let
.
Indeed, with some abuse of notation, let 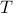 be a matrix defined as
be a matrix defined as 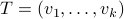 , for
, for 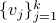 , the vertices of
, the vertices of  .
.
Before we continue, we need to establish some differential geometric results. Given the Special Orthogonal group 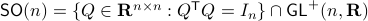 , the tangent space is given by
, the tangent space is given by 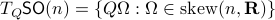 . Note, this is the explicit formulation, which is indeed equivalent to shifting the corresponding Lie Algebra.
The easiest way to compute this is to look at the kernel of the map defining the underlying manifold.
. Note, this is the explicit formulation, which is indeed equivalent to shifting the corresponding Lie Algebra.
The easiest way to compute this is to look at the kernel of the map defining the underlying manifold.
Now, following Brockett, consider the function 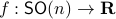 defined by
defined by 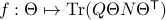 for some
for some 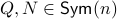 . This approach is not needed for the full construction, but it allows for more intuition and more computations.
To construct the corresponding gradient flow, recall that the (Riemannian) gradient at
. This approach is not needed for the full construction, but it allows for more intuition and more computations.
To construct the corresponding gradient flow, recall that the (Riemannian) gradient at 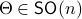 is defined via
is defined via ![df(Theta)[V]=langle mathrm{grad},f(Theta), Vrangle_{Theta}](eqs/666734593389601294-130.png) for all
for all 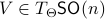 . Using the explicit tangent space representation, we know that
. Using the explicit tangent space representation, we know that 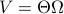 with
with 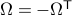 .
Then, see that by using
.
Then, see that by using
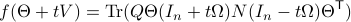
we obtain the gradient via
![df(Theta)[V]=lim_{tdownarrow 0}frac{f(Theta+tV)-f(Theta)}{t} = langle QTheta N, Theta Omega rangle - langle Theta N Theta^{mathsf{T}} Q Theta, Theta Omega rangle.](eqs/2651725126600601485-130.png)
This means that (the minus is missing in the paper) the (a) gradient flow becomes
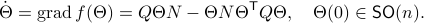
Consider the standard commutator bracket ![[A,B]=AB-BA](eqs/2726051070798907854-130.png) and see that for
and see that for 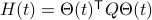 one obtains from the equation above (typo in the paper)
one obtains from the equation above (typo in the paper)
![dot{H}(t) = [H(t),[H(t),N]],quad H(0)=Theta^{mathsf{T}}QThetaquad (2).](eqs/8308117426617579905-130.png)
Hence,  can be seen as a reparametrization of a gradient flow.
It turns out that
can be seen as a reparametrization of a gradient flow.
It turns out that  has a variety of remarkable properties. First of all, see that
has a variety of remarkable properties. First of all, see that 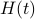 preserves the eigenvalues of
preserves the eigenvalues of  .
Also, observe the relation between extremizing
.
Also, observe the relation between extremizing  and the function
and the function 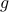 defined via
defined via 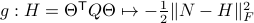 . The idea to handle LPs is now that the limiting
. The idea to handle LPs is now that the limiting 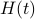 will relate to putting weight one the correct vertex to get the optimizer,
will relate to putting weight one the correct vertex to get the optimizer,  gives you this weight as it will contain the corresponding largest costs.
gives you this weight as it will contain the corresponding largest costs.
In fact, the matrix 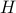 can be seen as an element of the set
can be seen as an element of the set 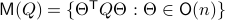 .
This set is in fact a
.
This set is in fact a 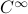 -smooth compact manifold as it can be written as the orbit space corresponding to the group action
-smooth compact manifold as it can be written as the orbit space corresponding to the group action 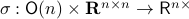 ,
,
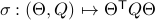 , one can check that this map satisfies the group properties. Hence, to extremize
, one can check that this map satisfies the group properties. Hence, to extremize 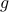 over
over 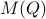 , it appears to be appealing to look at Riemannian optimization tools indeed. When doing so, it is convenient to understand the tangent space of
, it appears to be appealing to look at Riemannian optimization tools indeed. When doing so, it is convenient to understand the tangent space of 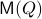 . Consider the map defining the manifold
. Consider the map defining the manifold 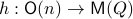 ,
, 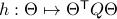 . Then by the construction of
. Then by the construction of 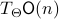 , see that
, see that ![dh(Theta)[V]=0](eqs/8898228761859333701-130.png) yields the relation
yields the relation ![[H,Omega]=0](eqs/197549272010137556-130.png) for any
for any 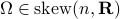 .
.
For the moment, let 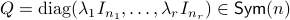 such that
such that  and
and 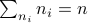 .
First we consider the convergence of
.
First we consider the convergence of  .
Let
.
Let  have only distinct eigenvalues, then
have only distinct eigenvalues, then 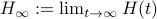 exists and is diagonal.
Using the objective
exists and is diagonal.
Using the objective  from before, consider
from before, consider 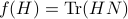 and see that by using the skew-symmetry one recovers the following
and see that by using the skew-symmetry one recovers the following
![begin{array}{lll} frac{d}{dt}mathrm{Tr}(H(t)N) &=& mathrm{Tr}(N [H,[H,N]]) &=& -mathrm{Tr}((HN-NH)^2) &=& |HN-NH|_F^2. end{array}](eqs/6018522323896655448-130.png)
This means the cost monotonically increases, but by compactness converges to some point 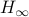 . By construction, this point must satisfy
. By construction, this point must satisfy ![[H_{infty},N]=0](eqs/5408610946697229240-130.png) . As
. As  has distinct eigenvalues, this can only be true if
has distinct eigenvalues, this can only be true if 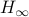 itself is diagonal (due to the distinct eigenvalues).
itself is diagonal (due to the distinct eigenvalues).
More can be said about 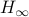 , let
, let 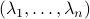 be the eigenvalues of
be the eigenvalues of 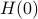 , that is, they correspond to the eigenvalues of
, that is, they correspond to the eigenvalues of  as defined above.
Then as
as defined above.
Then as 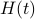 preserves the eigenvalues of
preserves the eigenvalues of  (
(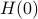 ), we must have
), we must have 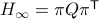 , for
, for 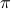 a permutation matrix.
This is also tells us there is just a finite number of equilibrium points (finite number of permutations). We will write this sometimes as
a permutation matrix.
This is also tells us there is just a finite number of equilibrium points (finite number of permutations). We will write this sometimes as 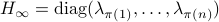 .
.
Now as  is one of those points, when does
is one of those points, when does 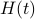 converge to
converge to  ? To start this investigation, we look at the linearization of
? To start this investigation, we look at the linearization of  , which at an equilibrium point
, which at an equilibrium point  becomes
becomes
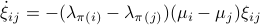
for 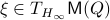 . As we work with matrix-valued vector fields, this might seems like a duanting computation. However, at equilibrium points one does not need a connection and can again use the directional derivative approach, in combination with the construction of
. As we work with matrix-valued vector fields, this might seems like a duanting computation. However, at equilibrium points one does not need a connection and can again use the directional derivative approach, in combination with the construction of 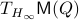 , to figure out the linearization. The beauty is that from there one can see that
, to figure out the linearization. The beauty is that from there one can see that  is the only asymptotically stable equilibrium point of
is the only asymptotically stable equilibrium point of  . Differently put, almost all initial conditions
. Differently put, almost all initial conditions 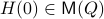 will converge to
will converge to  with the rate captured by spectral gaps in
with the rate captured by spectral gaps in  and
and  . If
. If  does not have distinct eigenvalues and we do not impose any eigenvalue ordering on
does not have distinct eigenvalues and we do not impose any eigenvalue ordering on  , one sees that an asymptotically stable equilibrium point
, one sees that an asymptotically stable equilibrium point 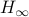 must have the same eigenvalue ordering as
must have the same eigenvalue ordering as  . This is the sorting property of the isospectral flow and this is of use for the next and final statement.
. This is the sorting property of the isospectral flow and this is of use for the next and final statement.
Theorem:
Consider the LP  with
with 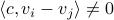 for all
for all ![i,jin [k]](eqs/5752860898065984697-130.png) , then, there exist diagonal matrices
, then, there exist diagonal matrices  and
and  such that
such that  converges for almost any
converges for almost any 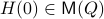 to
to 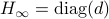 with the optimizer of
with the optimizer of  being
being 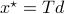 .
.
Proof:
Global convergence is prohibited by the topology of 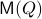 .
Let
.
Let 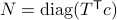 and let
and let 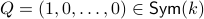 . Then, the isospectral flow will converge from almost everywhere to
. Then, the isospectral flow will converge from almost everywhere to  (only
(only 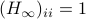 ), such that
), such that 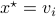 .
.
Please consider the references for more on the fascinating structure of  .
.
The Imaginary trick |12 March 2021|
tags: math.OC
Most of us will learn at some point in our life that 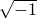 is problematic, as which number multiplied by itself can ever be negative?
To overcome this seemingly useless defiency one learns about complex numbers and specifically, the imaginary number
is problematic, as which number multiplied by itself can ever be negative?
To overcome this seemingly useless defiency one learns about complex numbers and specifically, the imaginary number 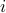 , which is defined to satisfy
, which is defined to satisfy 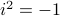 .
At this point you should have asked yourself when on earth is this useful?
.
At this point you should have asked yourself when on earth is this useful?
In this short post I hope to highlight - from a slightly different angle most people grounded in physics would expect - that the complex numbers are remarkably useful.
Complex numbers, and especially the complex exponential, show up in a variety of contexts, from signal processing to statistics and quantum mechanics. With of course most notably, the Fourier transformation.
We will however look at something completely different. It can be argued that in the late 60s James Lyness and Cleve Moler brought to life a very elegant new approach to numerical differentiation. To introduce this idea, recall that even nowadays the most well-known approach in numerical differentiation is to use some sort of finite-difference method, for example, for any  one could use the central-difference method
one could use the central-difference method
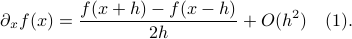
Now one might be tempted to make 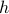 extremely small, as then the error must vanish!
However, numerically, for a very small
extremely small, as then the error must vanish!
However, numerically, for a very small 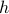 the two function evaluations
the two function evaluations 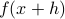 and
and 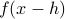 will be indistinguishable.
So although the error scales as
will be indistinguishable.
So although the error scales as 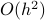 there is some practical lower bound on this error based on the machine precision of your computer.
One potential application of numerical derivatives is in the context of zeroth-order (derivative-free) optimization.
Say you want to adjust van der Poel his Canyon frame such that he goes even faster, you will not have access to explicit gradients, but you can evaluate the performance of a change in design, for example in a simulator. So what you usually can obtain is a set of function evaluations
there is some practical lower bound on this error based on the machine precision of your computer.
One potential application of numerical derivatives is in the context of zeroth-order (derivative-free) optimization.
Say you want to adjust van der Poel his Canyon frame such that he goes even faster, you will not have access to explicit gradients, but you can evaluate the performance of a change in design, for example in a simulator. So what you usually can obtain is a set of function evaluations 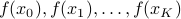 . Given this data, a somewhat obvious approach is to mimick first-order algorithms
. Given this data, a somewhat obvious approach is to mimick first-order algorithms
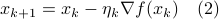
where 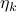 is some stepsize. For example, one could replace
is some stepsize. For example, one could replace 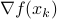 in
in  by the central-difference approximation
by the central-difference approximation  .
Clearly, if the objective function
.
Clearly, if the objective function  is well-behaved and the approximation of
is well-behaved and the approximation of 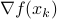 is reasonably good, then something must come out?
As was remarked before, if your approximation - for example due to numerical cancellation errors - will always have a bias it is not immediate how to construct a high-performance zeroth-order optimization algorithm. Only if there was a way to have a numerical approximation without finite differencing?
is reasonably good, then something must come out?
As was remarked before, if your approximation - for example due to numerical cancellation errors - will always have a bias it is not immediate how to construct a high-performance zeroth-order optimization algorithm. Only if there was a way to have a numerical approximation without finite differencing?
Let us assume that 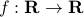 is sufficiently smooth, let
is sufficiently smooth, let 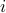 be the imaginary number and consider the following series
be the imaginary number and consider the following series
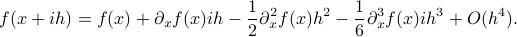
From this expression it follows that
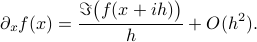
So we see that by passing to the complex domain and projecting the imaginary part back, we obtain a numerical method to construct approximations of derivatives without even the possibility of cancellation errors. This remarkable property makes it a very attractive candidate to be used in zeroth-order optimization algorithms, which is precisely what we investigated in our new pre-print. It turns out that convergence is not only robust, but also very fast!
Topological Considersations in Stability Analysis |17 November 2020|
tags: math.DS
In this post we discuss very classical, yet, highly underappreciated topological results.
We will look at dynamical control systems of the form
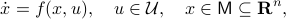
where  is some finite-dimensional embedded manifold.
is some finite-dimensional embedded manifold.
As it turns out, topological properties of  encode a great deal of fundamental control possibilities, most notably, if a continuous globally asymptotically stabilizing control law exists or not (usually, one can only show the negative). In this post we will work towards two things, first, we show that a technically interesting nonlinear setting is that of a dynamical system evolving on a compact manifold, where we will discuss that the desirable continuous feedback law can never exist, yet, the boundedness implied by the compactness does allow for some computations. Secondly, if one is determined to work on systems for which a continuous globally asymptotically stable feedback law exists, then a wide variety of existential sufficient conditions can be found, yet, the setting is effectively Euclidean, which is the most basic nonlinear setting.
encode a great deal of fundamental control possibilities, most notably, if a continuous globally asymptotically stabilizing control law exists or not (usually, one can only show the negative). In this post we will work towards two things, first, we show that a technically interesting nonlinear setting is that of a dynamical system evolving on a compact manifold, where we will discuss that the desirable continuous feedback law can never exist, yet, the boundedness implied by the compactness does allow for some computations. Secondly, if one is determined to work on systems for which a continuous globally asymptotically stable feedback law exists, then a wide variety of existential sufficient conditions can be found, yet, the setting is effectively Euclidean, which is the most basic nonlinear setting.
To start the discussion, we need one important topological notion.
Definition [Contractability].
Given a topological manifold 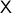 . If the map
. If the map 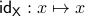 is null-homotopic, then,
is null-homotopic, then, 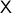 is contractible.
is contractible.
To say that a space is contractible when it has no holes (genus  ) is wrong, take for example the sphere. The converse is true, any finite-dimensional space with a hole cannot be contractible. See Figure 1 below.
) is wrong, take for example the sphere. The converse is true, any finite-dimensional space with a hole cannot be contractible. See Figure 1 below.
 |
Figure 1:
The manifold |
Topological Obstructions to Global Asymptotic Stability
In this section we highlight a few (not all) of the most elegant topological results in stability theory. We focus on results without appealing to the given or partially known vector field  .
This line of work finds its roots in work by Bhatia, Szegö, Wilson, Sontag and many others.
.
This line of work finds its roots in work by Bhatia, Szegö, Wilson, Sontag and many others.
Theorem [The domain of attraction is contractible, Theorem 21]
Let the flow 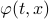 be continuous and let
be continuous and let 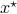 be an asymptotically stable equilibrium point. Then, the domain of attraction
be an asymptotically stable equilibrium point. Then, the domain of attraction 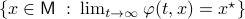 is contractible.
is contractible.
This theorem by Sontag states that the underlying topology of a dynamical system, better yet, the space on which the dynamical system evolves, dictates what is possible. Recall that linear manifolds are simply hyperplanes, which are contractible and hence, as we all know, global asymptotic stability is possible for linear systems. However, if  is not contractible, there does not exist a globally asymptotically stabilizable continuous-time system on
is not contractible, there does not exist a globally asymptotically stabilizable continuous-time system on  , take for example any sphere.
, take for example any sphere.
The next example shows that one should not underestimate ‘‘linear systems’’ either.
Example [Dynamical Systems on  ]
Recall that
]
Recall that  is a smooth
is a smooth 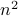 -dimensional manifold (Lie group).
Then, consider for some
-dimensional manifold (Lie group).
Then, consider for some 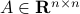 ,
, 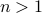 the (right-invariant) system
the (right-invariant) system
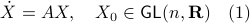
Indeed, the solution to (1) is given by 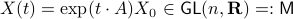 . Since this group consists out of two disjoint components there does not exist a matrix
. Since this group consists out of two disjoint components there does not exist a matrix  , or continuous nonlinear map for that matter, which can make a vector field akin to (1) globally asymptotically stable. This should be contrasted with the closely related ODE
, or continuous nonlinear map for that matter, which can make a vector field akin to (1) globally asymptotically stable. This should be contrasted with the closely related ODE 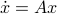 ,
, 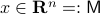 . Even for the path connected component
. Even for the path connected component 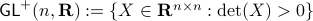 , The theorem by Sontag obstructs the existence of a continuous global asymptotically stable vector field. This because the group is not simply connected for
, The theorem by Sontag obstructs the existence of a continuous global asymptotically stable vector field. This because the group is not simply connected for 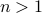 (This follows most easily from establishing the homotopy equivalence between
(This follows most easily from establishing the homotopy equivalence between 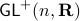 and
and 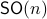 via (matrix) Polar Decomposition), hence the fundamental group is non-trivial and contractibility is out of the picture. See that if one would pick
via (matrix) Polar Decomposition), hence the fundamental group is non-trivial and contractibility is out of the picture. See that if one would pick  to be stable (Hurwitz), then for
to be stable (Hurwitz), then for 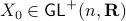 we have
we have 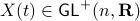 , however
, however 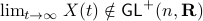 .
.
Following up on Sontag, Bhat and Bernstein revolutionized the field by figuring out some very important ramifications (which are easy to apply). The key observation is the next lemma (that follows from intersection theory arguments, even for non-orientable manifolds).
Lemma [Proposition 1] Compact, boundaryless, manifolds are never contractible.
Clearly, we have to ignore  -dimensional manifolds here. Important examples of this lemma are the
-dimensional manifolds here. Important examples of this lemma are the 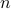 -sphere
-sphere 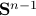 and the rotation group
and the rotation group 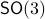 as they make a frequent appearance in mechanical control systems, like a robotic arm.
Note that the boundaryless assumption is especially critical here.
as they make a frequent appearance in mechanical control systems, like a robotic arm.
Note that the boundaryless assumption is especially critical here.
Now the main generalization by Bhat and Bernstein with respect to the work of Sontag is to use a (vector) bundle construction of  .
Loosely speaking, given a base
.
Loosely speaking, given a base 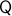 and total manifold
and total manifold  ,
,  is a vector bundle when for the surjective map
is a vector bundle when for the surjective map 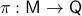 and each
and each 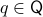 we have that the fiber
we have that the fiber 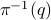 is a finite-dimensional vector space (see the great book by Abraham, Marsden and Ratiu Section 3.4 and/or the figure below).
is a finite-dimensional vector space (see the great book by Abraham, Marsden and Ratiu Section 3.4 and/or the figure below).
 |
Figure 2:
A prototypical vector bundle, in this case the cylinder |
Intuitively, vector bundles can be thought of as manifolds with vector spaces attached at each point, think of a cylinder living in  , where the base manifold is
, where the base manifold is  and each fiber is a line through
and each fiber is a line through 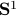 extending in the third direction, as exactly what the figure shows. Note, however, this triviality only needs to hold locally.
extending in the third direction, as exactly what the figure shows. Note, however, this triviality only needs to hold locally.
A concrete example is a rigid body with 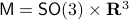 , for which a large amount of papers claim to have designed continuous globally asymptotically stable controllers. The fact that this was so enormously overlooked makes this topological result not only elegant from a mathematical point of view, but it also shows its practical value.
The motivation of this post is precisely to convey this message, topological insights can be very fruitful.
, for which a large amount of papers claim to have designed continuous globally asymptotically stable controllers. The fact that this was so enormously overlooked makes this topological result not only elegant from a mathematical point of view, but it also shows its practical value.
The motivation of this post is precisely to convey this message, topological insights can be very fruitful.
Now we can state their main result
Theorem [Theorem 1]
Let 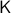 be a compact, boundaryless, manifold, being the base of the vector bundle
be a compact, boundaryless, manifold, being the base of the vector bundle 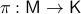 with
with 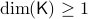 , then, there is no continuous vector field on
, then, there is no continuous vector field on  with a global asymptotically stable equilibrium point.
with a global asymptotically stable equilibrium point.
Indeed, compactness of 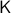 can also be relaxed to
can also be relaxed to 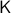 not being contractible as we saw in the example above, however, compactness is in most settings more tangible to work with.
not being contractible as we saw in the example above, however, compactness is in most settings more tangible to work with.
Example [The Grassmannian manifold]
The Grassmannian manifold, denoted by 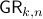 , is the set of all
, is the set of all 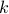 -dimensional subspaces
-dimensional subspaces 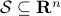 . One can identify
. One can identify 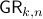 with the Stiefel manifold
with the Stiefel manifold 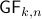 , the manifold of all orthogonal
, the manifold of all orthogonal 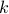 -frames, in the bundle sense of before, that is
-frames, in the bundle sense of before, that is 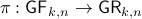 such that the fiber
such that the fiber 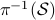 represent all
represent all 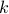 -frames generating the subspace
-frames generating the subspace 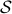 . In its turn,
. In its turn, 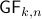 can be indentified with the compact Lie group
can be indentified with the compact Lie group 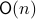 (via a quotient), such that indeed
(via a quotient), such that indeed 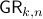 is compact.
This manifold shows up in several optimization problems and from our continuous-time point of view we see that one can never find, for example, a globally converging gradient-flow like algorithm.
is compact.
This manifold shows up in several optimization problems and from our continuous-time point of view we see that one can never find, for example, a globally converging gradient-flow like algorithm.
Example [Tangent Bundles]
By means of a Lagrangian viewpoint, a lot of mechanical systems are of a second-order nature, this means they are defined on the tangent bundle of some 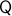 , that is,
, that is, 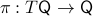 . However, then, if the configuration manifold
. However, then, if the configuration manifold 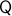 is compact, we can again appeal to the Theorem by Bhat and Bernstein. For example, Figure 2 can relate to the manifold over which the pair
is compact, we can again appeal to the Theorem by Bhat and Bernstein. For example, Figure 2 can relate to the manifold over which the pair 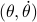 is defined.
is defined.
Global Isomorphisms
One might wonder, given a vector field  over a manifold
over a manifold  , since we need contractibility of
, since we need contractibility of  for
for  to have a global asymptotically stable equilibrium points, how interesting are these manifolds? As it turns out, for
to have a global asymptotically stable equilibrium points, how interesting are these manifolds? As it turns out, for 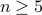 , which some might call the high-dimensional topological regime, contractible manifolds have a particular structure.
, which some might call the high-dimensional topological regime, contractible manifolds have a particular structure.
A topological space  being simply connected is equivalent to the corresponding fundamental group being trivial. However, to highlight the work by Stallings, we need a slightly less well-known notion.
being simply connected is equivalent to the corresponding fundamental group being trivial. However, to highlight the work by Stallings, we need a slightly less well-known notion.
Definition [Simply connected at infinity]
The topological space  is simply connected at infinity, when for any compact subset
is simply connected at infinity, when for any compact subset  there exists a
there exists a  where
where 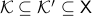 such that
such that 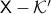 is simply connected.
is simply connected.
This definition is rather complicated to parse, however, we can give a more tangible description. Let  be a non-compact topological space, then,
be a non-compact topological space, then,  is said to have one end when for any compact
is said to have one end when for any compact  there is a
there is a 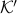 where
where 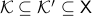 such that
such that 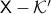 is connected. So,
is connected. So, 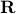 , as expected, fails to have one end, while
, as expected, fails to have one end, while 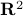 does have one end.
Now, Proposition 2.1 shows that if
does have one end.
Now, Proposition 2.1 shows that if 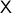 and
and 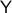 are simply connected and both have one end, then
are simply connected and both have one end, then 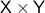 is simply connected at infinity. This statement somewhat clarifies why dimension
is simply connected at infinity. This statement somewhat clarifies why dimension 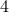 and above are somehow easier to parse in the context of topology. A similar statement can be made about the cylindrical space
and above are somehow easier to parse in the context of topology. A similar statement can be made about the cylindrical space 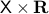 .
.
Lemma [Product representation Proposition 2.4]
Let  and
and  be manifolds of dimension greater or equal than
be manifolds of dimension greater or equal than  . If
. If 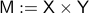 is contractible and
is contractible and 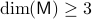 , then,
, then,  is simply connected at infinity.
is simply connected at infinity.
Now, most results are usually stated in the context of a piecewise linear (PL) topology. By appealing to celebrated results on triangulization (by Whitehead) we can state the following.
Theorem [Global diffeomorphism Theorem 5.1]
Let  be a contractible
be a contractible 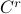 ,
, 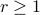 ,
, 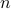 -dimensional manifold which is simply connected at infinity. If
-dimensional manifold which is simply connected at infinity. If 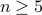 , then,
, then,  is diffeomorphic to
is diffeomorphic to 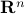 .
.
 |
Figure 3:
The manifold |
You might say that this is all obvious, as in Figure 3, we can always do it, also for lower-dimensions. However, there is famous counterexample by Whitehead, which provided lots of motivation for the community:
‘‘There is an open, 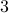 -dimensional manifold which is contractible, but not homeomorphic to
-dimensional manifold which is contractible, but not homeomorphic to 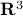 .’’
.’’
In fact, this example was part of the now notorious program to solve the Poincaré conjecture. All in all, this shows that contractible manifolds are not that interesting from a nonlinear dynamical systems point of view, compact manifolds is a class of manifolds providing for more of a challenge.
Remark on the Stabilization of Sets
So far, the discussion has been on the stabilization of (equilibrium) points, now what if we want to stabilize a curve or any other desirable set, that is, a non-trivial set 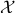 . It seems like the shape of these objects, with respect to the underlying topology of
. It seems like the shape of these objects, with respect to the underlying topology of  , must indicate if this is possible again? Let
, must indicate if this is possible again? Let 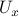 denote an open neighbourhood of some
denote an open neighbourhood of some 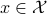 . In what follows, the emphasis is on
. In what follows, the emphasis is on 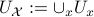 and
and 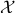 having the same topology. We will be brief and follow Moulay and Bhat.
having the same topology. We will be brief and follow Moulay and Bhat.
Lemma [Theorem 5]
Consider a closed-loop dynamical system given rise to a continuous flow. Suppose that the compact set  is asymptotically stable with domain of attraction
is asymptotically stable with domain of attraction  . Then,
. Then,  is a weak deformation retract of
is a weak deformation retract of  .
.
In rather loose terms,  being a weak deformation retract of
being a weak deformation retract of  means that one can continuously ‘‘retract’’ points from
means that one can continuously ‘‘retract’’ points from  and morph them into the set
and morph them into the set  . So, this works for
. So, this works for 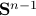 and
and 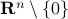 , due to
, due to  being punctured. See p.200 for more information on retracts. In Figure 4 below we show that since this lemma is mostly concerned with the local topology, the global topology is less important. For
being punctured. See p.200 for more information on retracts. In Figure 4 below we show that since this lemma is mostly concerned with the local topology, the global topology is less important. For  , the set
, the set 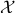 is not a deformation retract of the set
is not a deformation retract of the set 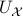 such that
such that  can never be a region of attraction, this should be contrasted with the setting on the Torus
can never be a region of attraction, this should be contrasted with the setting on the Torus  .
.
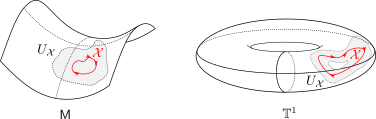 |
Figure 4:
The topological relation between |
The beauty of all of this is that even if you are not so sure about the exact dynamical system at hand, the underlying topology can already provide for some answers. In particular, to determine, what can, or cannot be done.
This post came about during a highly recommended course at EPFL.
Endomorphisms, Tensors in Disguise |18 August 2020|
tags: math.LA
Unfortunately the radio silence remained, the good news is that even more cool stuff is on its way*!
For now, we briefly mention a very beautiful interpretation of  -tensors.
Given some vectorspace
-tensors.
Given some vectorspace  , let
, let 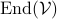 be the set of linear endomorphisms from
be the set of linear endomorphisms from  to
to  .
Indeed, for finite-dimensional vector spaces one can just think of these maps as being parametrized by matrices.
Now, we recall that
.
Indeed, for finite-dimensional vector spaces one can just think of these maps as being parametrized by matrices.
Now, we recall that 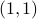 -tensors are multilinear maps which take an element of
-tensors are multilinear maps which take an element of  and its dual space
and its dual space 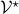 and map it to some real number, that is,
and map it to some real number, that is, 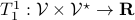 .
.
The claim is that for finite-dimensional  the set
the set 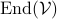 is isomorphic to the set of
is isomorphic to the set of 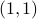 -tensors
-tensors 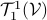 . This is rather intuitive to see, let
. This is rather intuitive to see, let 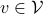 and
and 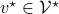 , then, we can write
, then, we can write 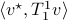 and think of
and think of 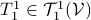 as a matrix. This can be formalized, as is done here by showing there is a bijective map
as a matrix. This can be formalized, as is done here by showing there is a bijective map 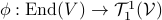 .
So, we can identify any
.
So, we can identify any 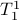 with some
with some 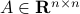 , that is
, that is 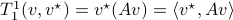 . Similarly, we can fix
. Similarly, we can fix 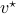 and identify
and identify 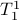 with a linear map in the dual space, that is
with a linear map in the dual space, that is 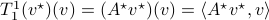 . Regardless, both represent the same tensor evaluation, hence
. Regardless, both represent the same tensor evaluation, hence
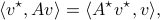
which is indeed the standard dual map definition.
Now we use this relation, recall that discrete-time linear systems are nothing more than maps 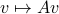 , that is, linear endomorphims, usually on
, that is, linear endomorphims, usually on 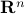 . Using the tensor interpretation we recover what is sometimes called the ‘‘dual system’’ to
. Using the tensor interpretation we recover what is sometimes called the ‘‘dual system’’ to 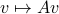 , namely
, namely 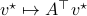 (suggestive notation indeed). Using more traditional notation for the primal:
(suggestive notation indeed). Using more traditional notation for the primal: 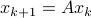 and dual:
and dual: 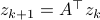 system, we recover that
system, we recover that 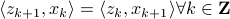 . Then, let
. Then, let  and
and  for
for 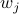 and
and 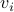 being a left- and right-eigenvector of
being a left- and right-eigenvector of  , respectively. We see that this implies that
, respectively. We see that this implies that 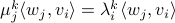 , for
, for 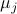 the eigenvalue corresponding to
the eigenvalue corresponding to 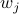 and
and 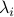 the eigenvalue corresponding to
the eigenvalue corresponding to 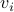 . Hence, in general, the eigenspaces of
. Hence, in general, the eigenspaces of  and
and 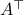 are generically orthogonal.
are generically orthogonal.
In other words, we recover the geometric interpretation of mapping 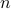 -volumes under
-volumes under  versus
versus 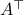 .
.
* See this talk by Daniel.
Optimal coordinates |24 May 2020|
tags: math.LA, math.OC, math.DS
There was a bit of radio silence, but as indicated here, some interesting stuff is on its way.
In this post we highlight this 1976 paper by Mullis and Roberts on ’Synthesis of Minimum Roundoff Noise Fixed Point Digital Filters’.
Let us be given some single-input single-output (SISO) dynamical system 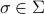
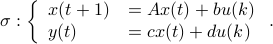
It is known that the input-output behaviour of any 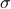 , that is, the map from
, that is, the map from 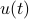 to
to 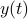 is invariant under a similarity transform.
To be explicit, the tuples
is invariant under a similarity transform.
To be explicit, the tuples 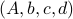 and
and 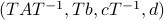 , which correspond to the change of coordinates
, which correspond to the change of coordinates 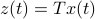 for some
for some 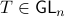 , give rise to the same input-output behaviour.
Hence, one can define the equivalence relation
, give rise to the same input-output behaviour.
Hence, one can define the equivalence relation  by imposing that the input-output maps of
by imposing that the input-output maps of 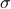 and
and 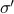 are equivalent.
By doing so we can consider the quotient
are equivalent.
By doing so we can consider the quotient  . However, in practice, given a
. However, in practice, given a 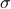 , is any
, is any 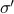 such that
such that 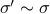 equally useful?
For example, the following
equally useful?
For example, the following  and
and  are similar, but clearly,
are similar, but clearly,  is preferred from a numerical point of view:
is preferred from a numerical point of view:
![A = left[begin{array}{ll} 0.5 & 10^9 0 & 0.5 end{array}right],quad A' = left[begin{array}{ll} 0.5 & 1 0 & 0.5 end{array}right].](eqs/6214495422406291774-130.png)
In what follows, we highlight the approach from Mullis and Roberts and conclude by how to optimally select 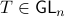 . Norms will be interpreted in the
. Norms will be interpreted in the 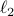 sense, that is, for
sense, that is, for 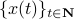 ,
, 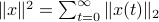 . Also, in what follows we assume that
. Also, in what follows we assume that 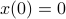 plus that
plus that  is stable, which will mean
is stable, which will mean 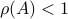 and that
and that  corresponds to a minimal realization.
corresponds to a minimal realization.
The first step is to quantify the error. Assume we have allocated 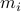 bits at our disposal to present the
bits at our disposal to present the 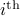 component of
component of 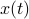 . These values for
. These values for 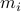 can differ, but we constrain the average by
can differ, but we constrain the average by 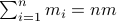 for some
for some 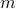 . Let
. Let 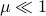 be a 'step-size’, such that our dynamic range of
be a 'step-size’, such that our dynamic range of 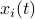 is bounded by
is bounded by 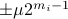 (these are our possible representations). Next we use the modelling choices from Mullis and Roberts, of course, they are debatable, but still, we will infer some nice insights.
(these are our possible representations). Next we use the modelling choices from Mullis and Roberts, of course, they are debatable, but still, we will infer some nice insights.
First, to bound the dynamic range, consider solely the effect of an input, that is, define 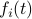 by
by 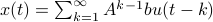 ,
, 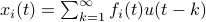 . Then we will impose the bound
. Then we will impose the bound 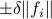 on
on 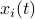 . In combination with the step size (quantization), this results in
. In combination with the step size (quantization), this results in 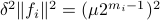 . Let
. Let  be a sequence of i.i.d. sampled random variables from
be a sequence of i.i.d. sampled random variables from  . Then we see that
. Then we see that 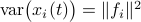 . Hence, one can think of
. Hence, one can think of  as scaling parameter related to the probability with which this dynamic range bound is true.
as scaling parameter related to the probability with which this dynamic range bound is true.
Next, assume that all the round-off errors are independent and have a variance of  .
Hence, the worst-case variance of computating
.
Hence, the worst-case variance of computating  is
is 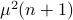 . To evaluate the effect of this error on the output, assume for the moment that
. To evaluate the effect of this error on the output, assume for the moment that 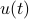 is identically
is identically  .
Then,
.
Then, 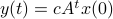 . Similar to
. Similar to 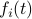 , define
, define 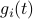 as the
as the 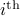 component of
component of 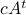 . As before we can compute the variance, this time of the full output signal, which yields
. As before we can compute the variance, this time of the full output signal, which yields
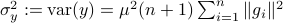 . Note, these expressions hinge on the indepedence assumption.
. Note, these expressions hinge on the indepedence assumption.
Next, define the (infamous) matrices 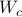 ,
, 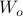 by
by
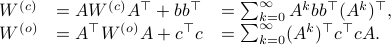
If we assume that the realization is not just minimal, but that  is a controllable pair and that
is a controllable pair and that 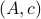 is an observable pair, then,
is an observable pair, then, 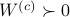 and
and 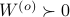 .
Now the key observation is that
.
Now the key observation is that 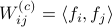 and similarly
and similarly 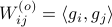 .
Hence, we can write
.
Hence, we can write 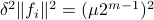 as
as 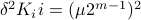 and indeed
and indeed 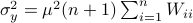 .
Using these Lyapunov equations we can say goodbye to the infinite-dimensional objects.
.
Using these Lyapunov equations we can say goodbye to the infinite-dimensional objects.
To combine these error terms, let say we have apply a coordinate transformation 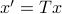 , for some
, for some 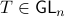 .
Specifically, let
.
Specifically, let 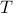 be diagonal and defined by
be diagonal and defined by 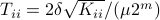 .
Then one can find that
.
Then one can find that 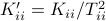 ,
, 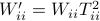 . Where the latter expressions allows to express the output error (variance) by
. Where the latter expressions allows to express the output error (variance) by
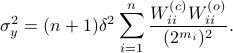
Now we want to minimize 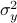 over all
over all 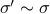 plus some optimal selection of
plus some optimal selection of 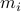 . At this point it looks rather painful. To make it work we first reformulate the problem using the well-known arithmetic-geometric mean inequality
. At this point it looks rather painful. To make it work we first reformulate the problem using the well-known arithmetic-geometric mean inequality![^{[1]}](eqs/2708305882951756665-130.png) for non-negative sequences
for non-negative sequences ![{a_i}_{iin [n]}](eqs/351138265746961916-130.png) :
:
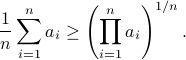
This inequality yields
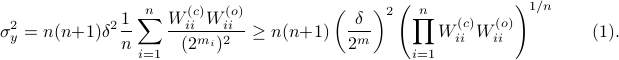
See that the right term is independent of  , hence this is a lower-bound with respect to minimization over
, hence this is a lower-bound with respect to minimization over  . To achieve this (to make the inequality from
. To achieve this (to make the inequality from  an equality), we can select
an equality), we can select
Indeed, as remarked in the paper,  is not per se an integer. Nevertheless, by this selection we find the clean expression from
is not per se an integer. Nevertheless, by this selection we find the clean expression from  to minimize over systems equivalent to
to minimize over systems equivalent to 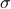 , that is, over some transformation matrix
, that is, over some transformation matrix  . Define a map
. Define a map ![f:mathcal{S}^n_{succ 0}to (0,1]](eqs/6462334851245421111-130.png) by
by
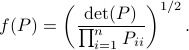
It turns out that 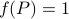 if and only if
if and only if 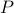 is diagonal. This follows
is diagonal. This follows![^{[2]}](eqs/2708306882823756034-130.png) from Hadamard's inequality.
We can use this map to write
from Hadamard's inequality.
We can use this map to write
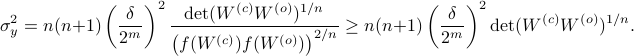
Since the term 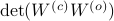 is invariant under a transformation
is invariant under a transformation 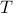 , we can only optimize
, we can only optimize 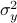 over a structural change in realization tuple
over a structural change in realization tuple 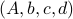 , that is, we need to make
, that is, we need to make 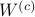 and
and 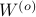 simultaneous diagonal! It turns out that this numerically 'optimal’ realization, denoted
simultaneous diagonal! It turns out that this numerically 'optimal’ realization, denoted 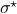 , is what is called a principal axis realization.
, is what is called a principal axis realization.
To compute it, diagonalize 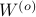 ,
, 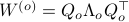 and define
and define 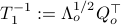 . Next, construct the diagonalization
. Next, construct the diagonalization 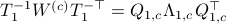 . Then our desired transformation is
. Then our desired transformation is 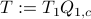 . First, recall that under any
. First, recall that under any  the pair
the pair  becomes
becomes 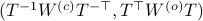 . Plugging in our map
. Plugging in our map 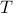 yields the transformed matrices
yields the transformed matrices  , which are indeed diagonal.
, which are indeed diagonal.
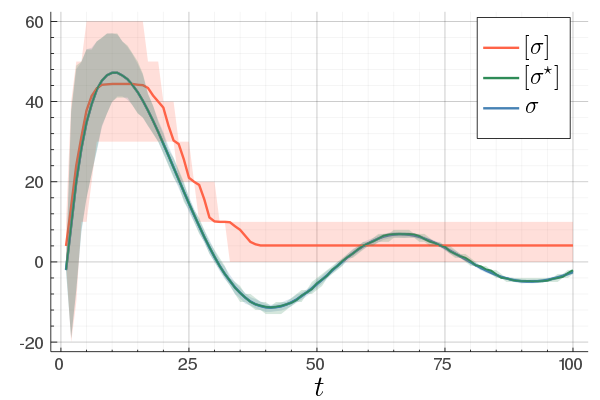 |
At last, we do a numerical test in Julia. Consider a linear system ![A = left[begin{array}{ll} 0.8 & 0.001 0 & -0.5 end{array} right],quad b = left[begin{array}{l} 10 0.1 end{array} right],](eqs/3623138148766993767-130.png)
![c=left[begin{array}{ll} 10 & 0.1 end{array} right],quad d=0.](eqs/42331078943303768-130.png)
To simulate numerical problems, we round the maps |
![[1]](eqs/8209412804330245758-130.png) : To show this AM-GM inequality, we can use Jensen's inequality for concave functions, that is,
: To show this AM-GM inequality, we can use Jensen's inequality for concave functions, that is, ![mathbf{E}[g(x)]leq g(mathbf{E}[x])](eqs/8492979742681909343-130.png) . We can use the logarithm as our prototypical concave function on
. We can use the logarithm as our prototypical concave function on 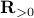 and find
and find 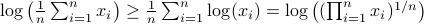 . Then, the result follows.
. Then, the result follows.
![[2]](eqs/8209412804333245623-130.png) : The inequality attributed to Hadamard is slightly more difficult to show. In its general form the statement is that
: The inequality attributed to Hadamard is slightly more difficult to show. In its general form the statement is that 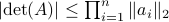 , for
, for 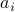 the
the 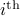 column of
column of  . The inequality becomes an equality when the columns are mutually orthogonal. The intuition is clear if one interprets the determinant as the signed volume spanned by the columns of
. The inequality becomes an equality when the columns are mutually orthogonal. The intuition is clear if one interprets the determinant as the signed volume spanned by the columns of  , which. In case
, which. In case 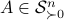 , we know that there is
, we know that there is  such that
such that 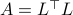 , hence, by this simple observation it follows that
, hence, by this simple observation it follows that
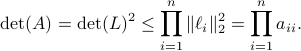
Equality holds when the columns are orthogonal, so  must be diagonal, but
must be diagonal, but  must also hold, hence,
must also hold, hence,  must be diagonal, and thus
must be diagonal, and thus  must be diagonal, which is the result we use.
must be diagonal, which is the result we use.
A Peculiar Lower Bound to the Spectral Radius |7 March 2020|
tags: math.LA
As a follow up to the previous post, we discuss a lower bound, given as exercise P7.1.14 in (GvL13).
I have never seen this bound before, especially not with the corresponding proof, so here we go.
Given any 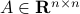 , we have the following lower bound:
, we have the following lower bound:
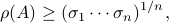
which can be thought of as a sharpening of the bound 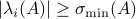 .
In the case of a singular
.
In the case of a singular  , the bound is trivial
, the bound is trivial 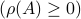 , but in the general setting it is less obvious.
To prove that this holds we need a few ingredients. First, we need that for any
, but in the general setting it is less obvious.
To prove that this holds we need a few ingredients. First, we need that for any 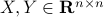 we have
we have 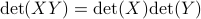 .
Then, we construct two decompositions of
.
Then, we construct two decompositions of  , (1) the Jordan Normal form
, (1) the Jordan Normal form 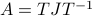 , and (2) the Singular Value Decomposition
, and (2) the Singular Value Decomposition 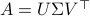 .
Using the multiplicative property of the determinant, we find that
.
Using the multiplicative property of the determinant, we find that
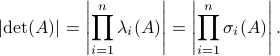
Hence, since 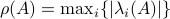 it follows that
it follows that 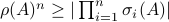 and thus we have the desired result.
and thus we have the desired result.
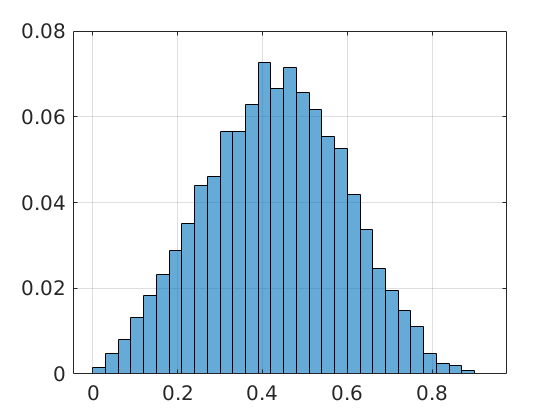 |
(Update 8 March) It is of course interesting to get insight in how sharp this bound is, in general. To that end we consider random matrices |
(GvL13) G.H. Golub and C.F. Van Loan: ‘‘Matrix Computations’’, 2013 John Hopkins University Press.
Spectral Radius vs Spectral Norm |28 Febr. 2020|
tags: math.LA, math.DS
Lately, linear discrete-time control theory has start to appear in areas far beyond the ordinary. As a byproduct, papers start to surface which claim that stability of linear discrete-time systems
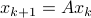
is characterized by 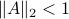 .
The confunsion is complete by calling this object the spectral norm of a matrix
.
The confunsion is complete by calling this object the spectral norm of a matrix 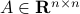 .
Indeed, for fixed coordinates, stability of
.
Indeed, for fixed coordinates, stability of  is not characterized by
is not characterized by 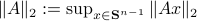 , but by
, but by ![rho(A):=max_{iin [n]}|lambda_i(A)|](eqs/8716262940618826552-130.png) .
If
.
If 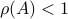 , then, all absolute eigenvalues of
, then, all absolute eigenvalues of  are strictly smaller than one, and hence for
are strictly smaller than one, and hence for 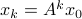 ,
, 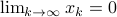 .
This follows from the Jordan form of
.
This follows from the Jordan form of  in combination with the simple observation that for
in combination with the simple observation that for 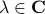 ,
, 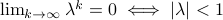 .
.
To continue, define two sets; 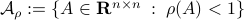 and
and 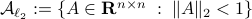 .
Since
.
Since![^{[1]}](eqs/2708305882951756665-130.png)
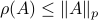 we have
we have 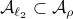 . Now, the main question is, how much do we lose by approximating
. Now, the main question is, how much do we lose by approximating  with
with 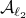 ? Motivation to do so is given by the fact that
? Motivation to do so is given by the fact that 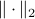 is a norm and hence a convex function
is a norm and hence a convex function![^{[2]}](eqs/2708306882823756034-130.png) , i.e., when given a convex polytope
, i.e., when given a convex polytope  with vertices
with vertices 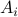 , if
, if 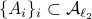 , then
, then 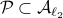 . Note that
. Note that 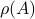 is not a norm,
is not a norm, 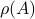 can be
can be  without
without 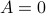 (consider an upper-triangular matrix with zeros on the main diagonal), the triangle inequality can easily fail as well. For example, let
(consider an upper-triangular matrix with zeros on the main diagonal), the triangle inequality can easily fail as well. For example, let
![A_1 = left[begin{array}{ll} 0 & 1 0 & 0 end{array}right], quad A_2 = left[begin{array}{ll} 0 & 0 1 & 0 end{array}right],](eqs/6730715665771009175-130.png)
Then 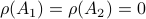 , but
, but 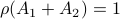 , hence
, hence 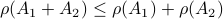 fails to hold.
A setting where the aforementioned property of
fails to hold.
A setting where the aforementioned property of  might help is Robust Control, say we want to assess if some algorithm rendered a compact convex set
might help is Robust Control, say we want to assess if some algorithm rendered a compact convex set  , filled with
, filled with  's, stable.
As highlighted before, we could just check if all extreme points of
's, stable.
As highlighted before, we could just check if all extreme points of  are members of
are members of  , which might be a small and finite set.
Thus, computationally, it appears to be attractive to consider
, which might be a small and finite set.
Thus, computationally, it appears to be attractive to consider  over the generic
over the generic  .
.
As a form of critique, one might say that  is a lot larger than
is a lot larger than 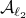 .
Towards such an argument, one might recall that
.
Towards such an argument, one might recall that 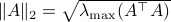 . Indeed,
. Indeed, 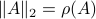 if
if![^{[3]}](eqs/2708307882947756447-130.png)
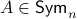 , but
, but 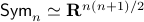 . Therefore, it seems like the set of
. Therefore, it seems like the set of  for which considering
for which considering  over
over  is reasonable, is negligibly small.
To say a bit more, since
is reasonable, is negligibly small.
To say a bit more, since![^{[4]}](eqs/2708308882819756064-130.png)
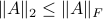 we see that we can always find a ball with non-zero volume fully contained in
we see that we can always find a ball with non-zero volume fully contained in  .
Hence,
.
Hence,  is at least locally dense in
is at least locally dense in 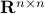 .
So in principle we could try to investigate
.
So in principle we could try to investigate  . For
. For  , the sets agree, which degrades asymptotically.
However, is this the way to go? Lets say we consider the set
, the sets agree, which degrades asymptotically.
However, is this the way to go? Lets say we consider the set  . Clearly, the sets
. Clearly, the sets 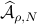 and
and  are different, even in volume, but for sufficiently large
are different, even in volume, but for sufficiently large 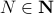 , should we care? The behaviour they parametrize is effectively the same.
, should we care? The behaviour they parametrize is effectively the same.
We will stress that by approximating  with
with 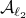 , regardless of their volumetric difference, we are ignoring a full class of systems and miss out on a non-neglible set of behaviours.
To see this, any system described by
, regardless of their volumetric difference, we are ignoring a full class of systems and miss out on a non-neglible set of behaviours.
To see this, any system described by 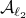 is contractive in the sense that
is contractive in the sense that 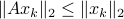 , while systems in
, while systems in  are merely asymptotically stable. They might wander of before they return, i.e., there is no reason why for all
are merely asymptotically stable. They might wander of before they return, i.e., there is no reason why for all 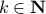 we must have
we must have 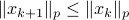 . We can do a quick example, consider the matrices
. We can do a quick example, consider the matrices
![A_2 = left[begin{array}{lll} 0 & -0.9 & 0.1 0.9 & 0 & 0 0 & 0 & -0.9 end{array}right], quad A_{rho} = left[begin{array}{lll} 0.1 & -0.9 & 1 0.9 & 0 & 0 0 & 0 & -0.9 end{array}right].](eqs/7939256391259616851-130.png)
Then 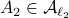 ,
, 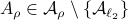 and both
and both 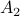 and
and 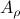 have
have 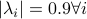 .
We observe that indeed
.
We observe that indeed 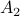 is contractive, for any initial condition on
is contractive, for any initial condition on 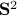 , we move strictly inside the sphere, whereas for
, we move strictly inside the sphere, whereas for 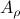 , when starting from the same initial condition, we take a detour outside of the sphere before converging to
, when starting from the same initial condition, we take a detour outside of the sphere before converging to  . So although
. So although 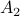 and
and 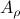 have the same spectrum, they parametrize different systems.
have the same spectrum, they parametrize different systems.
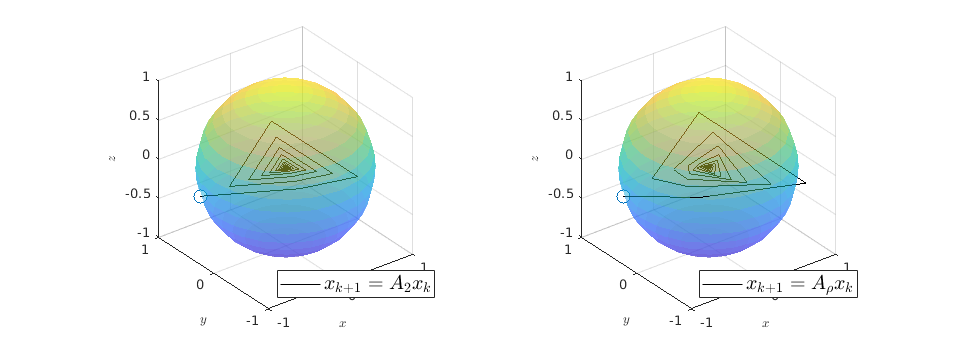 |
In our deterministic setting this would mean that we would confine our statespace to a (solid) sphere with radius 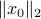 , instead of
, instead of 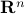 .
Moreover, in linear optimal control, the resulting closed-loop system is usually not contractive.
Think of the infamous pendulum on a cart. Being energy efficient has usually nothing to do with taking the shortest, in the Euclidean sense, path.
.
Moreover, in linear optimal control, the resulting closed-loop system is usually not contractive.
Think of the infamous pendulum on a cart. Being energy efficient has usually nothing to do with taking the shortest, in the Euclidean sense, path.
(update June 06): As suggested by Pedro Zattoni, we would like to add some nuance here. As highlighted in the first 12 minutes of this lecture by Pablo Parrilo, if  is stable, then, one can always find a (linear) change of coordinates such that the transformed system matrix is contractive. Although a very neat observation, you have to be careful, since your measurements might not come from this transformed system. So either you assume merely that
is stable, then, one can always find a (linear) change of coordinates such that the transformed system matrix is contractive. Although a very neat observation, you have to be careful, since your measurements might not come from this transformed system. So either you assume merely that  is stable, or you assume that
is stable, or you assume that  is contractive, but then you might need to find an additional map, mapping your states to your measurements.
is contractive, but then you might need to find an additional map, mapping your states to your measurements.
![[1]](eqs/8209412804330245758-130.png) : Recall,
: Recall, 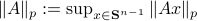 . Then, let
. Then, let 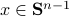 be some eigenvector of
be some eigenvector of  . Now we have
. Now we have 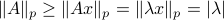 . Since this eigenvalue is arbitrary it follows that
. Since this eigenvalue is arbitrary it follows that 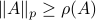 .
.
![[2]](eqs/8209412804333245623-130.png) : Let
: Let 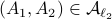 then
then 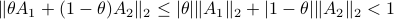 . This follows from the
. This follows from the  being a norm.
being a norm.
![[3]](eqs/8209412804332245752-130.png) : Clearly, if
: Clearly, if  , we have
, we have 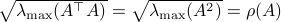 . Now, when
. Now, when 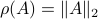 , does this imply that
, does this imply that  ? The answer is no, consider
? The answer is no, consider
![A' = left[begin{array}{lll} 0.9 & 0 & 0 0 & 0.1 & 0 0 & 0.1 & 0.1 end{array}right].](eqs/1479234184051328788-130.png)
Then,  , yet,
, yet, 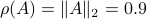 . For the full set of conditions on
. For the full set of conditions on  such that
such that 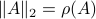 see this paper by Goldberg and Zwas.
see this paper by Goldberg and Zwas.
![[4]](eqs/8209412804335245617-130.png) : Recall that
: Recall that 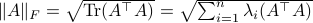 . This expression is clearly larger or equal to
. This expression is clearly larger or equal to 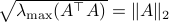 .
.
Risky Business in Stochastic Control: Exponential Utility |12 Jan. 2020|
tags: math.OC
One of the most famous problems in linear control theory is that of designing a control law which minimizes some cost being quadratic in input and state. We all know this as the Linear Quadratic Regulator (LQR) problem.
There is however one problem (some would call it a blessing) with this formulation once the dynamics contain some zero-mean noise: the control law is independent of this stochasticity. This is easy in proofs, easy in practice, but does it work well? Say, your control law is rather slow, but bringing you back to  in the end of time. In the noiseless case, no problem. But now say there is a substantial amount of noise, do you still want such a slow control law? The answer is most likely no since you quickly drift away. The classical LQR formulation does not differentiate between noise intensities and hence can be rightfully called naive as Bertsekas did (Bert76). Unfortunately, this name did not stuck.
in the end of time. In the noiseless case, no problem. But now say there is a substantial amount of noise, do you still want such a slow control law? The answer is most likely no since you quickly drift away. The classical LQR formulation does not differentiate between noise intensities and hence can be rightfully called naive as Bertsekas did (Bert76). Unfortunately, this name did not stuck.
Can we do better? Yes. Define the cost function
![gamma_{T-1}(theta) = frac{2}{theta T}log mathbf{E}_{xi}left[mathrm{exp}left(frac{theta}{2}sum^{T-1}_{t=0}x_t^{top}Qx_t + u_t^{top}Ru_t right) right]=frac{2}{theta T}log mathbf{E}_{xi}left[mathrm{exp}left(frac{theta}{2}Psi right) right]](eqs/6416747510437753707-130.png)
and consider the problem of finding the minimizing policy 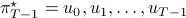 in:
in:
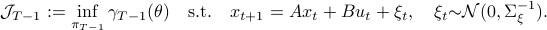
Which is precisely the classical LQR problem, but now with the cost wrapped in an exponential utility function parametrized by  .
This problem was pioneered by most notably Peter Whittle (Wh90).
.
This problem was pioneered by most notably Peter Whittle (Wh90).
Before we consider solving this problem, let us interpret the risk parameter  . For
. For 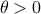 we speak of a risk-sensitive formulation while for
we speak of a risk-sensitive formulation while for 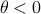 we are risk-seeking. This becomes especially clear when you solve the problem, but a quick way to see this is to consider the approximation of
we are risk-seeking. This becomes especially clear when you solve the problem, but a quick way to see this is to consider the approximation of 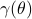 near
near 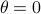 , which yields
, which yields ![gammaapprox mathbf{E}[Psi]+frac{1}{4}{theta}mathbf{E}[Psi]^2](eqs/7712769251826009795-130.png) , so
, so 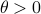 relates to pessimism and
relates to pessimism and 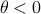 to optimism indeed. Here we skipped a few scaling factors, but the idea remains the same, for a derivation, consider cumulant generating functions and have a look at our problem.
to optimism indeed. Here we skipped a few scaling factors, but the idea remains the same, for a derivation, consider cumulant generating functions and have a look at our problem.
As with standard LQR, we would like to obtain a stabilizing policy and to that end we will be mostly bothered with solving  .
However, instead of immediately trying to solve the infinite horizon average cost Bellman equation it is easier to consider
.
However, instead of immediately trying to solve the infinite horizon average cost Bellman equation it is easier to consider 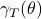 for finite
for finite 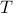 first. Then, when we can prove monotonicty and upper-bound
first. Then, when we can prove monotonicty and upper-bound 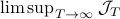 , the infinite horizon optimal policy is given by
, the infinite horizon optimal policy is given by 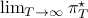 .
The reason being that monotonic sequences which are uniformly bounded converge.
.
The reason being that monotonic sequences which are uniformly bounded converge.
The main technical tool towards finding the optimal policy is the following Lemma similar to one in the Appendix of (Jac73):
Lemma 
Consider a noisy linear dynamical system defined by 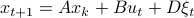 with
with 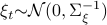 and let
and let 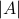 be shorthand notation for
be shorthand notation for 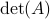 . Then, if
. Then, if 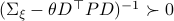 holds we have
holds we have
![mathbf{E}_{xi}left[mathrm{exp}left(frac{theta}{2}x_{k+1}^{top}Px_{k+1} right)|x_kright] = frac{|(Sigma_{xi}-theta D^{top}PD)^{-1}|^{1/2}}{|Sigma_{xi}^{-1}|^{1/2}}mathrm{exp}left(frac{theta}{2}(Ax_k+Bu_k)^{top}widetilde{P}(Ax_k+Bu_k) right)](eqs/8871996922177725349-130.png)
where
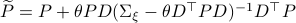 .
. 
Proof 
Let ![z:= mathbf{E}_{xi}left[mathrm{exp}left(frac{theta}{2}x_{t+1}^{top}Px_{t+1} right)|x_tright]](eqs/2205886115745182034-130.png) and recall that the shorthand notation for
and recall that the shorthand notation for  is
is  , then:
, then:
Here, the first step follows directly from  being a zero-mean Gaussian. In the second step we plug in
being a zero-mean Gaussian. In the second step we plug in  . Then, in the third step we introduce a variable
. Then, in the third step we introduce a variable  with the goal of making
with the goal of making 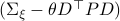 the covariance matrix of a Gaussian with mean
the covariance matrix of a Gaussian with mean 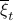 . We can make this work for
. We can make this work for
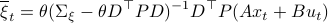
and additionally
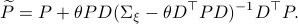
Using this approach we can integrate the latter part to  and end up with the final expression.
Note that in this case the random variable
and end up with the final expression.
Note that in this case the random variable 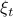 needs to be Gaussian, since the second to last expression in
needs to be Gaussian, since the second to last expression in  equals
equals  by being a Gaussian probability distribution integrated over its entire domain.
by being a Gaussian probability distribution integrated over its entire domain. 
What is the point of doing this?
Let 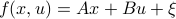 and assume that
and assume that 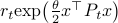 represents the cost-to-go from stage
represents the cost-to-go from stage 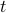 and state
and state 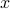 . Then consider
. Then consider
![r_{t-1}mathrm{exp}left(frac{theta}{2}x^{top}P_{t-1} xright) = inf_{u} left{mathrm{exp}left(frac{theta}{2}(x^{top}Qx+u^{top}Ru)right)mathbf{E}_{xi}left[r_tmathrm{exp}left( frac{theta}{2}f(x,u)^{top}P_{t}f(x,u)right);|;xright]right}.](eqs/8431854396343916570-130.png)
Note, since we work with a sum within the exponent, we must multiply within the right-hand-side of the Bellman equation.
From there it follows that
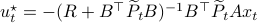 , for
, for
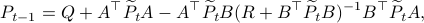
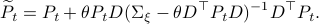
The key trick in simplifying your expressions is to apply the logarithm after minimizing over  such that the fraction of determinants becomes a state-independent affine term in the cost.
Now, using a matrix inversion lemma and the push-through rule we can remove
such that the fraction of determinants becomes a state-independent affine term in the cost.
Now, using a matrix inversion lemma and the push-through rule we can remove  and construct a map
and construct a map  :
:
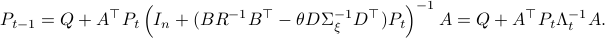
such that 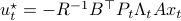 .
See below for the derivations, many (if not all) texts skip them, but if you have never applied the push-through rule they are not that obvious.
.
See below for the derivations, many (if not all) texts skip them, but if you have never applied the push-through rule they are not that obvious.
As was pointed out for the first time by Jacobson (Jac73), these equations are precisely the ones we see in (non-cooperative) Dynamic Game theory for isotropic 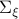 and appropriately scaled
and appropriately scaled 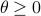 .
.
Especially with this observation in mind there are many texts which show that 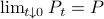 is well-defined and finite, which relates to finite cost and a stabilizing control law
is well-defined and finite, which relates to finite cost and a stabilizing control law 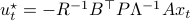 . To formalize this, one needs to assume that
. To formalize this, one needs to assume that  is a minimal realization for
is a minimal realization for  defined by
defined by 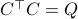 . Then you can appeal to texts like (BB95).
. Then you can appeal to texts like (BB95).
Numerical Experiment and Robustness Interpretation
To show what happens, we do a small  -dimensional example. Here we want to solve the Risk-Sensitive
-dimensional example. Here we want to solve the Risk-Sensitive 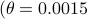 ) and the Risk-neutral (
) and the Risk-neutral (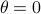 ) infinite-horizon average cost problem for
) infinite-horizon average cost problem for
![A = left[ begin{array}{ll} 2 & 1 0 & 2 end{array}right],quad B = left[ begin{array}{l} 0 1 end{array}right],quad Sigma_{xi}^{-1} = left[ begin{array}{ll} 10^{-1} & 200^{-1} 200^{-1} & 10 end{array}right],](eqs/5026564260006708683-130.png)
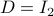 ,
, 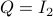 ,
,  .
There is clearly a lot of noise, especially on the second signal, which also happens to be critical for controlling the first state. This makes it interesting.
We compute
.
There is clearly a lot of noise, especially on the second signal, which also happens to be critical for controlling the first state. This makes it interesting.
We compute 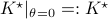 and
and 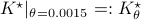 .
Given the noise statistics, it would be reasonable to not take the certainty equivalence control law
.
Given the noise statistics, it would be reasonable to not take the certainty equivalence control law 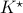 since you control the first state (which has little noise on its line) via the second state (which has a lot of noise on its line). Let
since you control the first state (which has little noise on its line) via the second state (which has a lot of noise on its line). Let 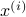 be the
be the 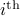 state under
state under 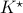 and
and 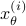 the
the  state under
state under 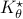 .
.
We see in the plot below (for some arbitrary initial condition) typical behaviour, 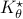 does take the noise into account and indeed we see the
does take the noise into account and indeed we see the  induces a smaller variance.
induces a smaller variance.
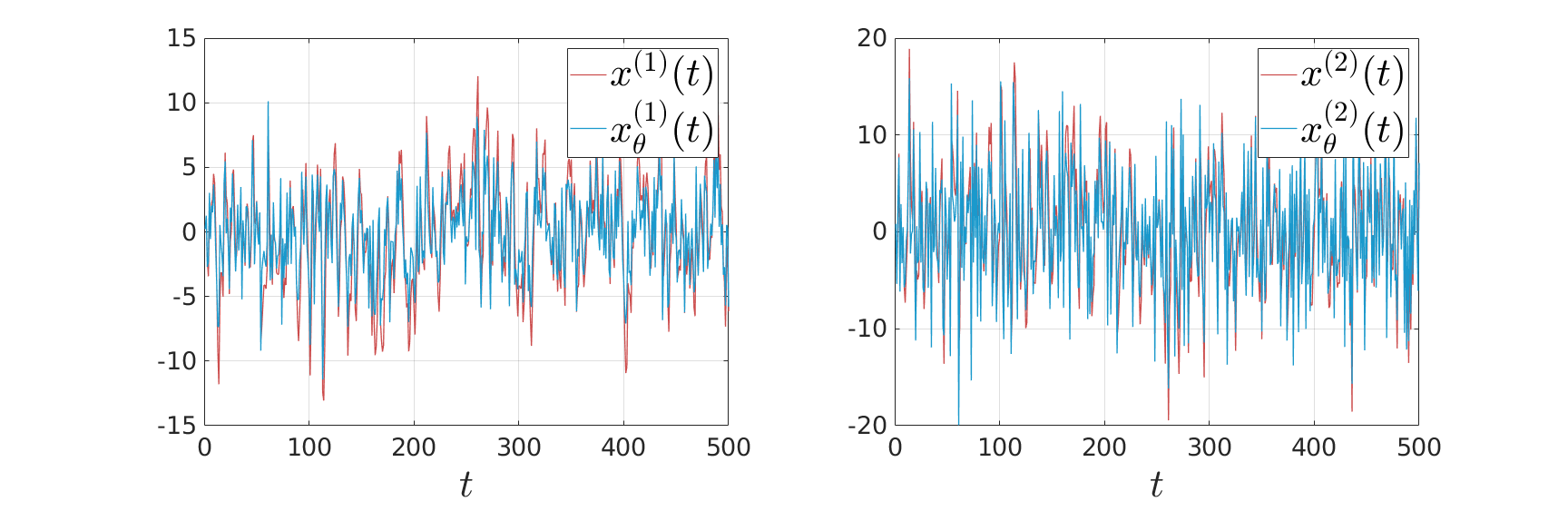 |
So,  is more robust than
is more robust than  in a particular way. It turns out that this can be neatly explained. To do so, we have to introduce the notion of Relative Entropy (Kullback-Leibler divergence). We will skip a few technical details (see the references for full details). Given a measure
in a particular way. It turns out that this can be neatly explained. To do so, we have to introduce the notion of Relative Entropy (Kullback-Leibler divergence). We will skip a few technical details (see the references for full details). Given a measure 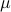 on
on  , then for any other measure
, then for any other measure 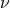 , being absolutely continuous with respect to
, being absolutely continuous with respect to 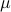 (
(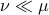 ), define the Relative Entropy as:
), define the Relative Entropy as:
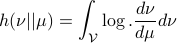
Now, for any measurable function  on
on  , being bounded from below, it can be shown (see (DP96)) that
, being bounded from below, it can be shown (see (DP96)) that
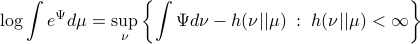
For the moment, think of  as your standard finite-horizon LQR cost with product measure
as your standard finite-horizon LQR cost with product measure 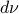 , then we see that an exponential utility results in the understanding that a control law which minimizes
, then we see that an exponential utility results in the understanding that a control law which minimizes 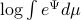 is robust against adversarial noise generated by distributions sufficiently close (measured by
is robust against adversarial noise generated by distributions sufficiently close (measured by  ) to the reference
) to the reference 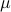 .
.
Here we skipped over a lot of technical details, but the intuition is beautiful, just changing the utility to the exponential function gives a wealth of deep distributional results we just touched upon in this post.
Simplification steps in 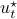
We only show to get the simpler representation for the input, the approach to obtain 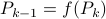 is very similar.
is very similar.
First, using the matrix inversion lemma:
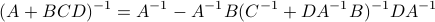
we rewrite 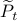 into:
into:
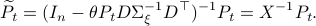
Note, we factored our  since we cannot assume that
since we cannot assume that 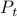 is invertible. Our next tool is called the push-through rule. Given
is invertible. Our next tool is called the push-through rule. Given  and
and 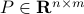 we have
we have
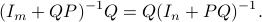
You can check that indeed 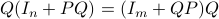 .
Now, to continue, plug this expression for
.
Now, to continue, plug this expression for  into the input expression:
into the input expression:
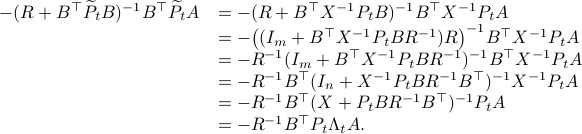
Indeed, we only used factorizations and the push-through rule to arrive here.
(Bert76) Dimitri P. Bertsekas : ‘‘Dynamic Programming and Stochastic Control’’, 1976 Academic Press.
(Jac73) D. Jacobson : ‘‘Optimal stochastic linear systems with exponential performance criteria and their relation to deterministic differential games’’, 1973 IEEE TAC.
(Wh90) Peter Whittle : ‘‘Risk-sensitive Optimal Control’’, 1990 Wiley.
(BB95) Tamer Basar and Pierre Bernhard : ‘‘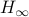 -Optimal Control and Related Minimax Design Problems A Dynamic Game Approach’’ 1995 Birkhauser.
-Optimal Control and Related Minimax Design Problems A Dynamic Game Approach’’ 1995 Birkhauser.
(DP96) Paolo Dai Pra, Lorenzo Meneghini and Wolfgang J. Runggaldier :‘‘Connections Between Stochastic Control and Dynamic Games’’ 1996 Math. Control Signals Systems.
Are Theo Jansen his Linkages Optimal? |16 Dec. 2019|
tags: math.OC
Theo Jansen, designer of the infamous ‘‘strandbeesten’’ explains in a relatively recent series of videos that the design of his linkage system is the result of what could be called an early implementation of genetic programming. Specifically, he wanted the profile that the foot follows to be flat on the bottom. He does not elaborate on this too much, but the idea is that in this way his creatures flow over the surface instead of the more bumpy motion we make. Moreover, you can imagine that in this way the center of mass remains more or less at a constant height, which is indeed energy efficient. Now, many papers have been written on understanding his structure, but I find most of them rather vague, so lets try a simple example.
To that end, consider just 1 leg, 1 linkage system as in the figure(s) below. We can write down an explicit expression for 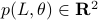 where
where 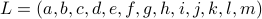 and
and 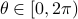 . See below for an explicit derivation. Now, with his motivation in mind, what would be an easy and relevant cost function? An idea is to maximize the ratio
. See below for an explicit derivation. Now, with his motivation in mind, what would be an easy and relevant cost function? An idea is to maximize the ratio  , of course, subject to still having a functioning leg. To that end we consider the cost function (see the schematic below for notation):
, of course, subject to still having a functioning leg. To that end we consider the cost function (see the schematic below for notation):
Of course, this is a heuristic, but the intuition is that this should approximate  .
Let
.
Let 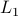 be the set of parameters as given in Jansen his video, then we apply a few steps of (warm-start) gradient ascent:
be the set of parameters as given in Jansen his video, then we apply a few steps of (warm-start) gradient ascent: 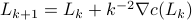 ,
, 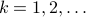 .
.
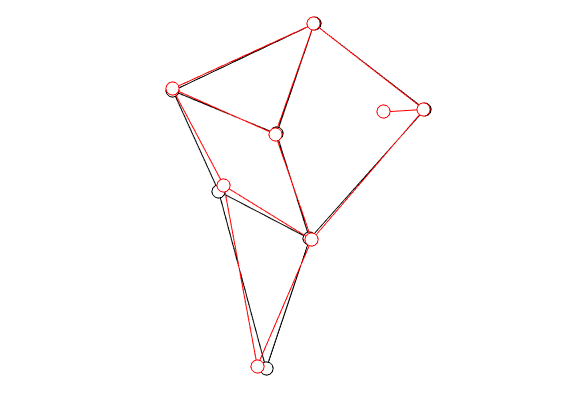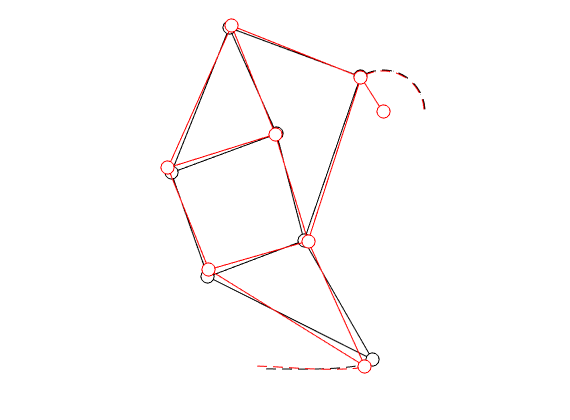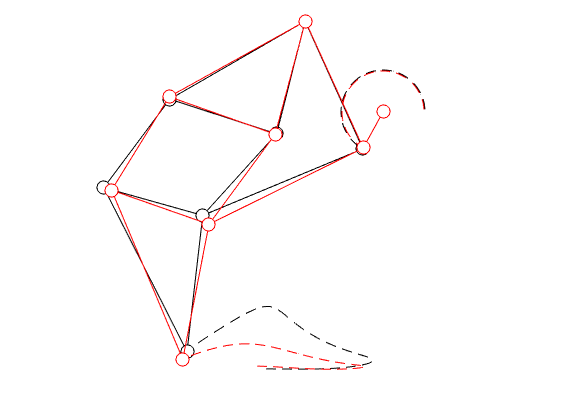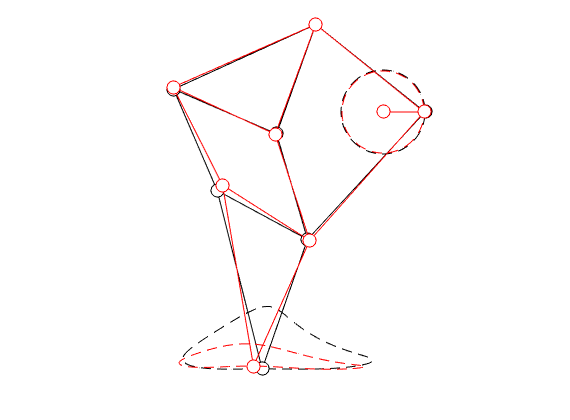 |
In the figure on the left we compare the linkage as given by Jansen (in black) with the result of just two steps of gradient ascent (in red).
You clearly see that the trajectory of the foot becomes more shallow. Nevertheless, we see that the profile starts to become curved on the bottom. It is actually interesting to note that |
Can we conclude anything from here? I would say that we need dynamics, not just kinematics, but more importantly, we need to put the application in the optimization and only Theo Jansen understands the constraints of the beach.
Still, it is fun to see for yourself how this works and like I did you can build a (baby) strandbeest yourself using nothing more than some PVC tubing and a source of heat.
Derivation of  :
:
Essentially, all that you need is the cosine-rule plus some feeling for how to make the equations continuous.
To start, let 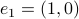 and
and 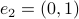 (just the standard unit vectors), plus let
(just the standard unit vectors), plus let 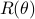 be a standard (counter-clockwise) rotation matrix acting on
be a standard (counter-clockwise) rotation matrix acting on 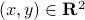 . To explain the main approach, when we want to find the coordinates of for example point
. To explain the main approach, when we want to find the coordinates of for example point 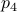 , we try to compute the angle
, we try to compute the angle 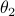 such that when we rotate the unit vector
such that when we rotate the unit vector 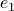 with length
with length 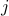 emanating from point
emanating from point 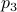 , we get point
, we get point 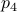 . See the schematic picture below.
. See the schematic picture below.
Then we easily obtain  ,
,  and
and 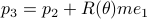 .
Now, to obtain
.
Now, to obtain 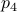 and
and  compute the length of the diagonal,
compute the length of the diagonal, 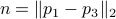 and using the cosine rule
and using the cosine rule 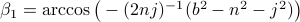 ,
, 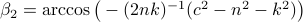 . Then, the trick is to use
. Then, the trick is to use  to compute
to compute  . To avoid angles larger than
. To avoid angles larger than 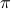 , consider an inner product with
, consider an inner product with 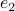 and add the remaining
and add the remaining 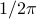 ;
; 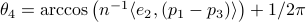 . From there we get
. From there we get 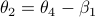 ,
, 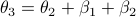 ,
, 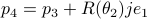 ,
, 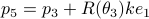 . The point
. The point 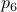 is not missing, to check your code it is convenient to compute
is not missing, to check your code it is convenient to compute 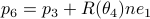 and check that
and check that 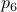 agrees with
agrees with 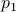 for all
for all 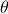 .
In a similar fashion,
.
In a similar fashion, 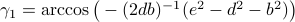 ,
, 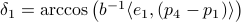 ,
, 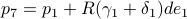 .
Then, for
.
Then, for 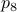 , again compute a diagonal
, again compute a diagonal 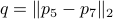 plus
plus 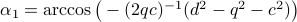 ,
, 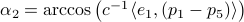
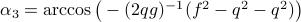 , such that for
, such that for 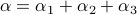 we have
we have 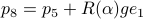 .
At last,
.
At last, 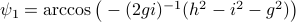 , such that
, such that 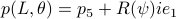 for
for 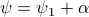 .
.
 |
A Special Group, Volume Preserving Feedback |16 Nov. 2019|
tags: math.LA, math.DS
This short note is inspired by the beautiful visualization techniques from Duistermaat and Kolk (DK1999) (themselves apparently inspired by Atiyah).
Let's say we have a  -dimensional linear discrete-time dynamical system
-dimensional linear discrete-time dynamical system 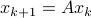 , which preserves the volume of the cube
, which preserves the volume of the cube ![[-1,1]^2](eqs/7220646983027292775-130.png) under the dynamics, i.e.
under the dynamics, i.e. ![mathrm{Vol}([-1,1]^2)=mathrm{Vol}(A^k[-1,1]^2)](eqs/6078350520623442645-130.png) for any
for any  .
.
Formally put, this means that  is part of a certain group, specifically, consider some field
is part of a certain group, specifically, consider some field 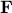 and
define the Special Linear group by
and
define the Special Linear group by
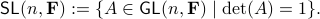
Now, assume that we are only interested in matrices 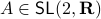 such that the cube
such that the cube ![[-1,1]^2](eqs/7220646983027292775-130.png) remains bounded under the dynamics, i.e.,
remains bounded under the dynamics, i.e., ![lim_{kto infty}A^k[-1,1]^2](eqs/6180125548835686349-130.png) is bounded. In this scenario we restrict our attention to
is bounded. In this scenario we restrict our attention to 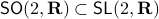 . To see why this is needed, consider
. To see why this is needed, consider  and
and  both with determinant
both with determinant  :
:
![A_1 = left[ begin{array}{ll} 2 & 0 0 & frac{1}{2} end{array}right], quad A_2 = left[ begin{array}{ll} 1 & 2 0 & 1 end{array}right],](eqs/4004660008936570769-130.png)
If we look at the image of ![[-1,1]^2](eqs/7220646983027292775-130.png) under both these maps (for several iterations), we see that volume is preserved, but also clearly that the set is extending indefinitely in the horizontal direction.
under both these maps (for several iterations), we see that volume is preserved, but also clearly that the set is extending indefinitely in the horizontal direction.
 |
To have a somewhat interesting problem, assume we are given 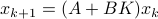 with
with 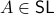 while it is our task to find a
while it is our task to find a 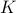 such that
such that 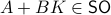 , hence, find feedback which not only preserves the volume, but keeps any set of initial conditions (say
, hence, find feedback which not only preserves the volume, but keeps any set of initial conditions (say ![[-1,1]^2](eqs/7220646983027292775-130.png) ) bounded over time.
) bounded over time.
Towards a solution, we might ask, given any 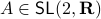 what is the nearest (in some norm) rotation matrix? This turns out to be a classic question, starting from orthogonal matrices, the solution to
what is the nearest (in some norm) rotation matrix? This turns out to be a classic question, starting from orthogonal matrices, the solution to 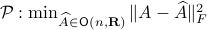 is given by
is given by 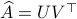 , where
, where 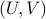 follows from the SVD of
follows from the SVD of  ,
, 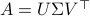 .
Differently put, when we use a polar decomposition of
.
Differently put, when we use a polar decomposition of  ,
, 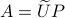 , then the solution is given by
, then the solution is given by 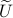 . See this note for a quick multiplier proof.
An interesting sidenote, problem
. See this note for a quick multiplier proof.
An interesting sidenote, problem 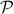 is well-defined since
is well-defined since 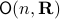 is compact. To see this, recall that for any
is compact. To see this, recall that for any 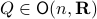 we have
we have 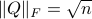 , hence the set is bounded, plus
, hence the set is bounded, plus 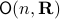 is the pre-image of
is the pre-image of 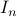 under
under 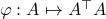 ,
, 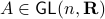 , hence the set is closed as well.
, hence the set is closed as well.
This is great, however, we would like to optimize over 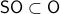 instead. To do so, one usually resorts to simply checking the sign - and if necessary - flipping it via finding the closest matrix with a change in determinant sign.
We will see that by selecting appropriate coordinates we can find the solution without this checking of signs.
instead. To do so, one usually resorts to simply checking the sign - and if necessary - flipping it via finding the closest matrix with a change in determinant sign.
We will see that by selecting appropriate coordinates we can find the solution without this checking of signs.
For today we look at 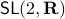 and largely follow (DK1999), for such a
and largely follow (DK1999), for such a  -dimensional matrix, the determinant requirement translates to
-dimensional matrix, the determinant requirement translates to 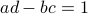 . Under the following (invertible) linear change of coordinates
. Under the following (invertible) linear change of coordinates
![left[ begin{array}{l} a d b c end{array}right] = left[ begin{array}{llll} 1 & 1 & 0 & 0 1 & -1 & 0 & 0 0 & 0 & 1 & 1 0 & 0 & 1 & -1 end{array}right] left[ begin{array}{l} p q r s end{array}right]](eqs/6118233270205082065-130.png)
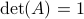 becomes
becomes 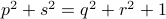 , i.e., for any pair
, i.e., for any pair 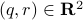 the point
the point 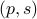 runs over a circle with radius
runs over a circle with radius 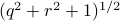 . Hence, we obtain the diffeomorphism
. Hence, we obtain the diffeomorphism 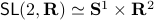 . We can use however a more pretty diffeomorphism of the sphere and an open set in
. We can use however a more pretty diffeomorphism of the sphere and an open set in 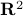 . To that end, use the diffeomorphism:
. To that end, use the diffeomorphism:
![(theta,(u,v)) mapsto frac{1}{sqrt{1-u^2-v^2}} left[ begin{array}{ll} cos(theta)+u & -sin(theta)+v sin(theta)+v & cos(theta)-u end{array}right] in mathsf{SL}(2,mathbf{R}),](eqs/6656969251929689946-130.png)
for 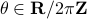 (formal way of declaring that
(formal way of declaring that 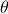 should not be any real number) and the pair
should not be any real number) and the pair  being part of
being part of 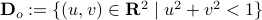 (the open unit-disk).
To see this, recall that the determinant is not a linear operator.
Since we have a
(the open unit-disk).
To see this, recall that the determinant is not a linear operator.
Since we have a  -dimensional example we can explicitly compute the eigenvalues of any
-dimensional example we can explicitly compute the eigenvalues of any 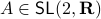 (plug
(plug 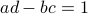 into the characteristic equation) and obtain:
into the characteristic equation) and obtain:
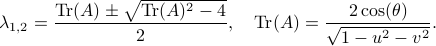
At this point, the only demand on the eigenvalues is that 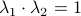 . Therefore, when we would consider
. Therefore, when we would consider  within the context of a discrete linear dynamical system
within the context of a discrete linear dynamical system 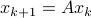 ,
,  is either a saddle-point, or we speak of a marginally stable system (
is either a saddle-point, or we speak of a marginally stable system (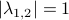 ).
We can visualize the set of all marginally stable
).
We can visualize the set of all marginally stable 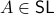 , called
, called 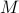 , defined by all
, defined by all 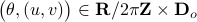 satisfying
satisfying
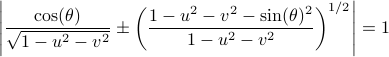
(DK1999) J.J. Duistermaat and J.A.C. Kolk : ‘‘Lie Groups’’, 1999 Springer.
Riemannian Gradient Flow |5 Nov. 2019|
tags: math.DG, math.DS
Previously we looked at  ,
, 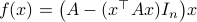 - and its resulting flow - as the result from mapping
- and its resulting flow - as the result from mapping 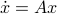 to the sphere. However, we saw that for
to the sphere. However, we saw that for 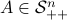 this flow convergences to
this flow convergences to  , with
, with 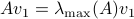 such that for
such that for 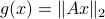 we have
we have 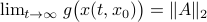
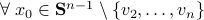 . Hence, it is interesting to look at the flow from an optimization point of view:
. Hence, it is interesting to look at the flow from an optimization point of view: 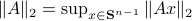 .
.
A fair question would be, is our flow not simply Riemannian gradient ascent for this problem? As common with these kind of problems, such a hypothesis is something you just feel.
Now, using the tools from (CU1994, p.311) we can compute the gradient of 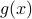 (on the sphere) via
(on the sphere) via 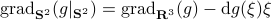 , where
, where 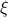 is a vector field normal to
is a vector field normal to 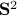 , e.g.,
, e.g., 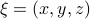 .
From there we obtain
.
From there we obtain
![mathrm{grad}_{mathbf{S}^2}(g|_{mathbf{S}^2}) = left[ begin{array}{lll} (1-x^2) & -xy & -xz -xy & (1-y^2) & -yz -xz & -yz & (1-z^2) end{array}right] left[ begin{array}{l}partial_x g partial_y g partial_z g end{array}right]=G(x,y,z)nabla g.](eqs/2499009703266316151-130.png)
To make our life a bit easier, use instead of 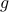 the map
the map 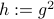 . Moreover, set
. Moreover, set 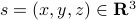 . Then it follows that
. Then it follows that
![begin{array}{ll} mathrm{grad}_{mathbf{S}^2}(h|_{mathbf{S}^2}) &= left(I_3-mathrm{diag}(s)left[begin{array}{l} s^{top}s^{top}s^{top} end{array}right]right) 2A^{top}As &= 2left(A^{top}A-(s^{top}A^{top}Asright)I_3)s. end{array}](eqs/2245781100057659571-130.png)
Of course, to make the computation cleaner, we changed 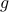 to
to 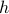 , but the relation between
, but the relation between 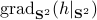 and
and  is beautiful. Somehow, mapping trajectories of
is beautiful. Somehow, mapping trajectories of 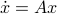 , for some
, for some 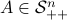 , to the sphere corresponds to (Riemannian) gradient ascent applied to the problem
, to the sphere corresponds to (Riemannian) gradient ascent applied to the problem 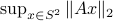 .
.
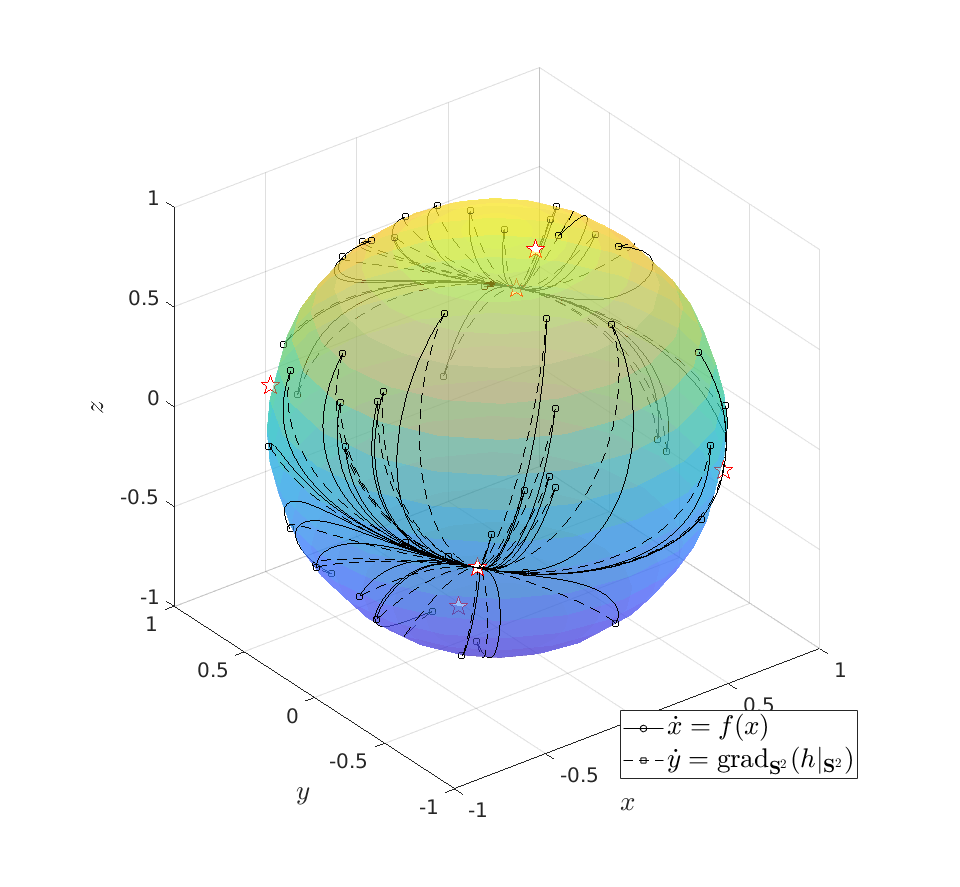 |
To do an example, let ![A = left[ begin{array}{lll} 10 & 2 & 0 2 & 10 & 2 0 & 2 & 1 end{array}right].](eqs/6133576945654762450-130.png)
We can compare |
Now, we formalize the previous analysis a bit a show how fast we convergence. Assume that the eigenvectors are ordered such that eigenvector 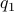 corresponds to the largest eigenvalue of
corresponds to the largest eigenvalue of 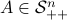 . Then, the solution to
. Then, the solution to 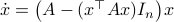 is given by
is given by
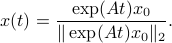
Let 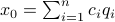 be
be 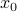 expressed in eigenvector coordinates, with all
expressed in eigenvector coordinates, with all 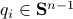 (normalized). Moreover, assume all eigenvalues are distinct. Then, to measure if
(normalized). Moreover, assume all eigenvalues are distinct. Then, to measure if 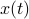 is near
is near 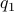 , we compute
, we compute 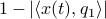 , which is
, which is  if and only if
if and only if 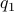 is parallel to
is parallel to 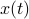 . To simplify the analysis a bit, we look at
. To simplify the analysis a bit, we look at 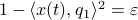 , for some perturbation
, for some perturbation 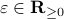 , this yields
, this yields
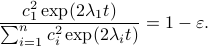
Next, take the the (natural) logarithm on both sides:
This log-sum-exp terms are hard to deal with, but we can apply the so-called ‘‘log-sum-exp trick’’:
In our case, we set 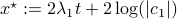 and obtain
and obtain
![-log left(sum^{n}_{i=1}exp left{2 left[(lambda_i-lambda_1)t + logleft(frac{|c_i|}{|c_1|} right) right] right}+1 right) = log(1-varepsilon).](eqs/3165375830294523712-130.png)
We clearly observe that for 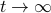 the LHS approaches
the LHS approaches  from below, which means that
from below, which means that 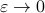 from above, like intended. Of course, we also observe that the mentioned method is not completely general, we already assume distinct eigenvalues, but there is more. We do also not convergence when
from above, like intended. Of course, we also observe that the mentioned method is not completely general, we already assume distinct eigenvalues, but there is more. We do also not convergence when  , which is however a set of measure
, which is however a set of measure  on the sphere
on the sphere 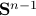 .
.
More interestingly, we see that the convergence rate is largely dictated by the ‘‘spectral gap/eigengap’’ 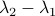 . Specifically, to have a particular projection error
. Specifically, to have a particular projection error  , such that
, such that  , we need
, we need
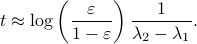
Comparing this to the resulting flow from 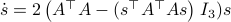 ,
, 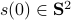 , we see that we have the same flow, but with
, we see that we have the same flow, but with 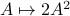 .
This is interesting, since
.
This is interesting, since  and
and 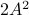 have the same eigenvectors, yet a different (scaled) spectrum. With respect to the convergence rate, we have to compare
have the same eigenvectors, yet a different (scaled) spectrum. With respect to the convergence rate, we have to compare 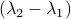 and
and 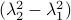 for any
for any  with
with  (the additional
(the additional  is not so interesting).
is not so interesting).
It is obvious what we will happen, the crux is, is 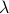 larger or smaller than
larger or smaller than  ? Can we immediately extend this to a Newton-type algorithm? Well, this fails (globally) since we work in
? Can we immediately extend this to a Newton-type algorithm? Well, this fails (globally) since we work in 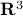 instead of purely with
instead of purely with 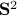 . To be concrete,
. To be concrete, 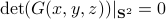 , we never have
, we never have 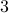 degrees of freedom.
degrees of freedom.
Of course, these observations turned out to be far from new, see for example (AMS2008, sec. 4.6).
(AMS2008) P.A. Absil, R. Mahony and R. Sepulchre: ‘‘Optimization Algorithms on Matrix Manifolds’’, 2008 Princeton University Press.
(CU1994) Constantin Udriste: ‘‘Convex Functions and Optimization Methods on Riemannian Manifolds’’, 1994 Kluwer Academic Publishers.
Simple Flow Algorithm to Compute the Operator Norm |4 Nov. 2019|
tags: math.LA
Using the ideas from the previous post, we immediately obtain a dynamical system to compute 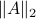 for any
for any 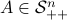 (symmetric positive definite matrices).
Here we use the vector field
(symmetric positive definite matrices).
Here we use the vector field 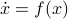 , defined by
, defined by 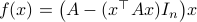 and denote a solution by
and denote a solution by  , where
, where  is the initial condition. Moreover, define a map
is the initial condition. Moreover, define a map  by
by 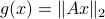 . Then
. Then 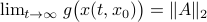
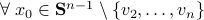 , where
, where 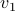 is the eigenvector corresponding to the largest eigenvalue.
is the eigenvector corresponding to the largest eigenvalue.
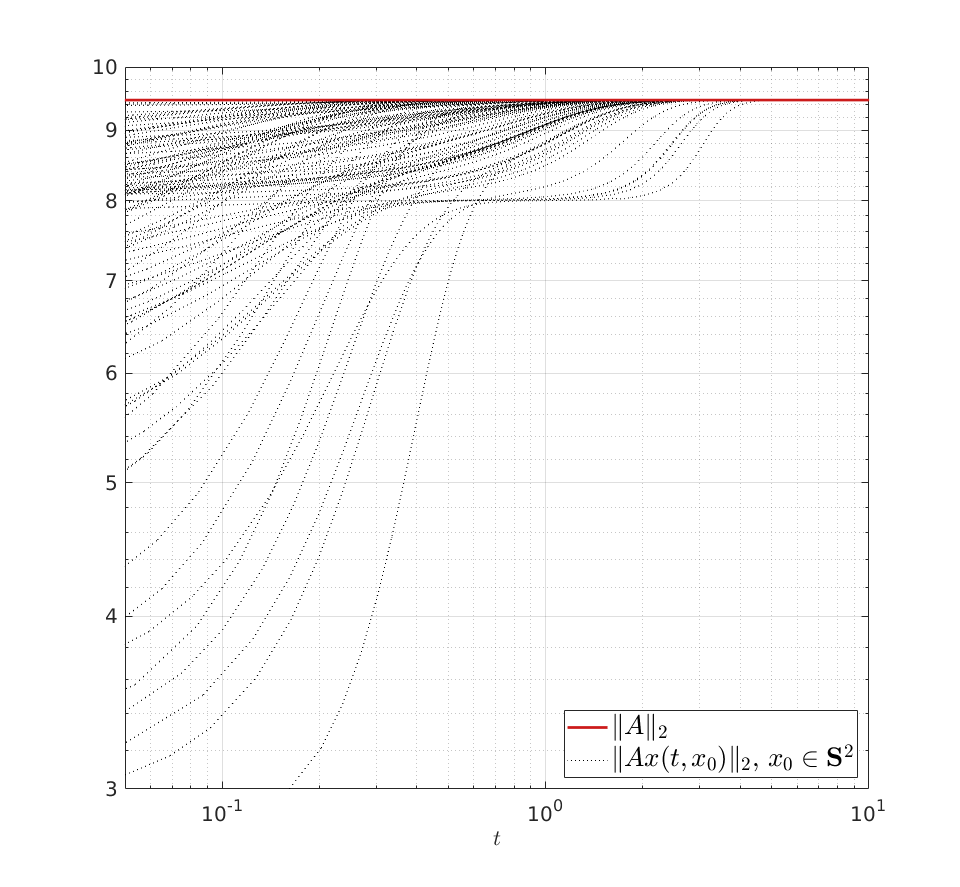 |
We can do a simple example, let ![A = left[ begin{array}{lll} 8 & 2 & 0 2 & 4 & 2 0 & 2 & 8 end{array}right]](eqs/3487469526425297871-130.png)
with |
Dynamical Systems on the Sphere |3 Nov. 2019|
tags: math.DS
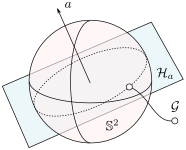 |
In this post we start a bit with control of systems living on compact metric spaces. This is interesting since we have to rethink what we want, |
To start, consider a linear dynamical systems 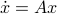 ,
, 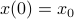 , for which the solution is given by
, for which the solution is given by 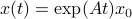 . We can map this solution to the sphere via
. We can map this solution to the sphere via 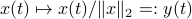 .
The corresponding vector field for
.
The corresponding vector field for 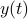 is given by
is given by
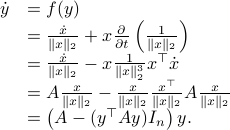
The beauty is the following, to find the equilibria, consider 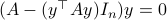 . Of course,
. Of course,  is not valid since
is not valid since 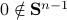 . However, take any eigenvector
. However, take any eigenvector  of
of  , then
, then 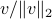 is still an eigenvector, plus it lives on
is still an eigenvector, plus it lives on 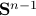 . If we plug such a scaled
. If we plug such a scaled  (from now on consider all eigenvectors to live on
(from now on consider all eigenvectors to live on 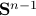 ) into
) into  we get
we get 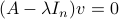 , which is rather cool. The eigenvectors of
, which is rather cool. The eigenvectors of  are (at least) the equilibria of
are (at least) the equilibria of 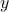 . Note, if
. Note, if 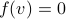 , then so is
, then so is 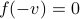 , each eigenvector gives rise to two equilibria.
We say at least, since if
, each eigenvector gives rise to two equilibria.
We say at least, since if 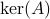 is non-trivial, then for any
is non-trivial, then for any 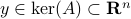 , we get
, we get 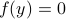 .
.
Let 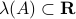 , then what can be said about the stability of the equilibrium points?
Here, we must look at
, then what can be said about the stability of the equilibrium points?
Here, we must look at 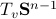 , where the
, where the 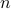 -dimensional system is locally a
-dimensional system is locally a 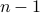 -dimensional linear system. To do this, we start by computing the standard Jacobian of
-dimensional linear system. To do this, we start by computing the standard Jacobian of  , which is given by
, which is given by
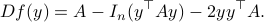
As said before, we do not have a 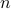 -dimensional system. To that end, we assume
-dimensional system. To that end, we assume 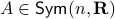 with diagonalization
with diagonalization 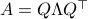 (otherwise peform a Gram-Schmidt procedure) and perform a change of basis
(otherwise peform a Gram-Schmidt procedure) and perform a change of basis 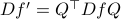 . Then if we are interested in the qualitative stability properties of
. Then if we are interested in the qualitative stability properties of  (the
(the 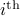 eigenvector of
eigenvector of  ), we can simply look at the eigenvalues of the matrix resulting from removing the
), we can simply look at the eigenvalues of the matrix resulting from removing the 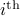 row and column in
row and column in 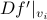 , denoted
, denoted 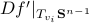 .
.
We do two examples. In both figures are the initial conditions indicated with a dot while the equilibrium points are stars.
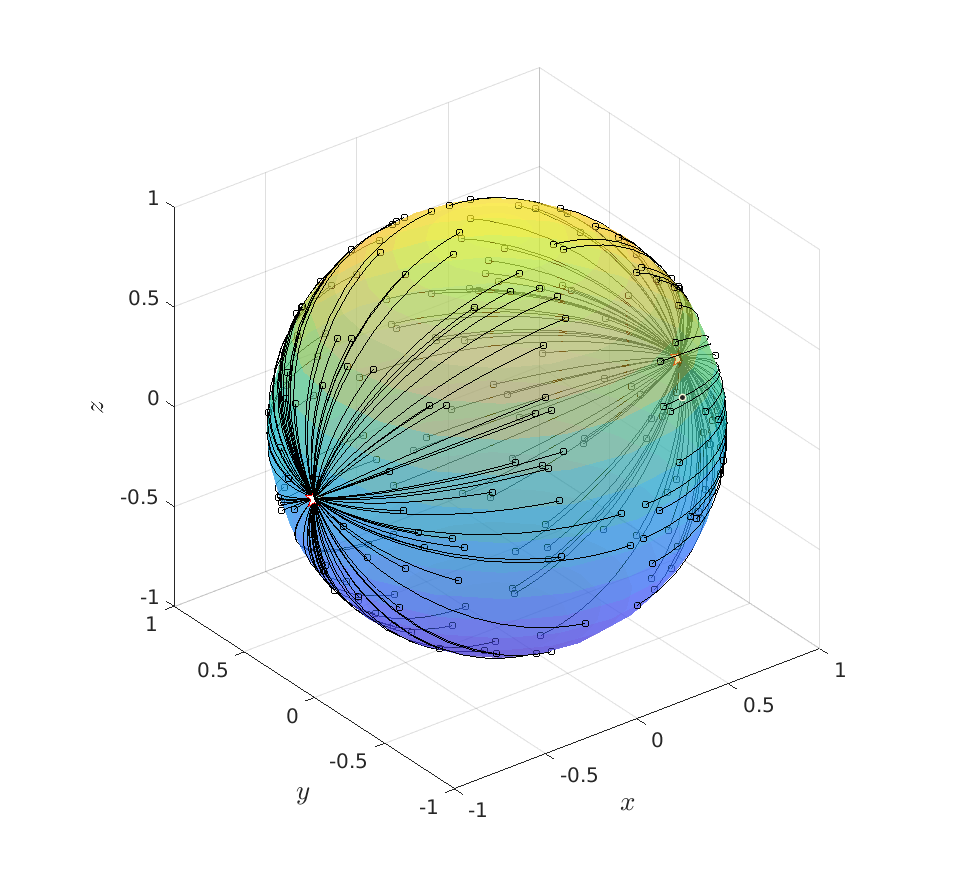 |
First, let ![A_1 = left[ begin{array}{lll} 1 & 0 & 0 0 & -1 & 0 0 & 0 & -1 end{array}right]](eqs/4948366788842116208-130.png)
Clearly, for |
Finite Calls to Stability | 31 Oct. 2019 |
tags: math.LA, math.DS
Consider an unknown dynamical system 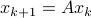 parametrized by
parametrized by 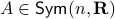 .
In this short note we look at a relatively simple, yet neat method to assess stability of
.
In this short note we look at a relatively simple, yet neat method to assess stability of  via finite calls to a particular oracle. Here, we will follow the notes by Roman Vershynin (RV2011).
via finite calls to a particular oracle. Here, we will follow the notes by Roman Vershynin (RV2011).
Assume we have no knowledge of  , but we are able to obtain
, but we are able to obtain 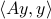 for any desired
for any desired 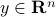 . It turns out that we can use this oracle to bound
. It turns out that we can use this oracle to bound 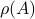 from above.
from above.
First, recall that since  is symmetric,
is symmetric, 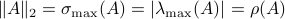 . Now, the common definition of
. Now, the common definition of 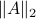 is
is 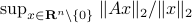 . The constraint set
. The constraint set  is not per se convenient from a computational point of view. Instead, we can look at a compact constraint set:
is not per se convenient from a computational point of view. Instead, we can look at a compact constraint set: 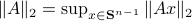 , where
, where 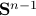 is the sphere in
is the sphere in 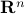 .
The latter formulation has an advantage, we can discretize these compact constraints sets and tame functions over the individual chunks.
.
The latter formulation has an advantage, we can discretize these compact constraints sets and tame functions over the individual chunks.
To do this formally, we can use  -nets, which are convenient in quantitative analysis on compact metric spaces
-nets, which are convenient in quantitative analysis on compact metric spaces 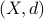 . Let
. Let 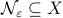 be a
be a  -net for
-net for  if
if 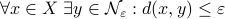 . Hence, we measure the amount of balls to cover
. Hence, we measure the amount of balls to cover  .
.
For example, take 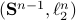 as our metric space where we want to bound
as our metric space where we want to bound 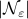 (the cardinality, i.e., the amount of balls). Then, to construct a minimal set of balls, consider an
(the cardinality, i.e., the amount of balls). Then, to construct a minimal set of balls, consider an  -net of balls
-net of balls 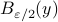 , with
, with 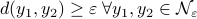 . Now the insight is simply that
. Now the insight is simply that 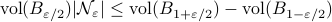 .
Luckily, we understand the volume of
.
Luckily, we understand the volume of 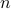 -dimensional Euclidean balls well such that we can establish
-dimensional Euclidean balls well such that we can establish
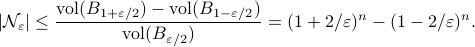
Which is indeed sharper than the bound from Lemma 5.2 in (RV2011).
Next, we recite Lemma 5.4 from (RV2011). Given an  -net for
-net for  with
with 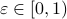 we have
we have
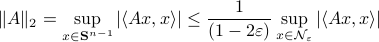
This can be shown using the Cauchy-Schwartz inequality. Now, it would be interesting to see how sharp this bound is.
To that end, we do a  -dimensional example (
-dimensional example ( ). Note, here we can easily find an optimal grid using polar coordinates. Let the unknown system be parametrized by
). Note, here we can easily find an optimal grid using polar coordinates. Let the unknown system be parametrized by
![A = left[ begin{array}{ll} 0.1 & -0.75 -0.75 & 0.1 end{array}right]](eqs/8870555444473195760-130.png)
such that  . In the figures below we compute the upper-bound to
. In the figures below we compute the upper-bound to 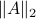 for several nets
for several nets 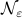 .
Indeed, for finer nets, we see the upper-bound approaching
.
Indeed, for finer nets, we see the upper-bound approaching 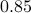 . However, we see that the convergence is slow while being inversely related to the exponential growth in
. However, we see that the convergence is slow while being inversely related to the exponential growth in 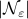 .
.
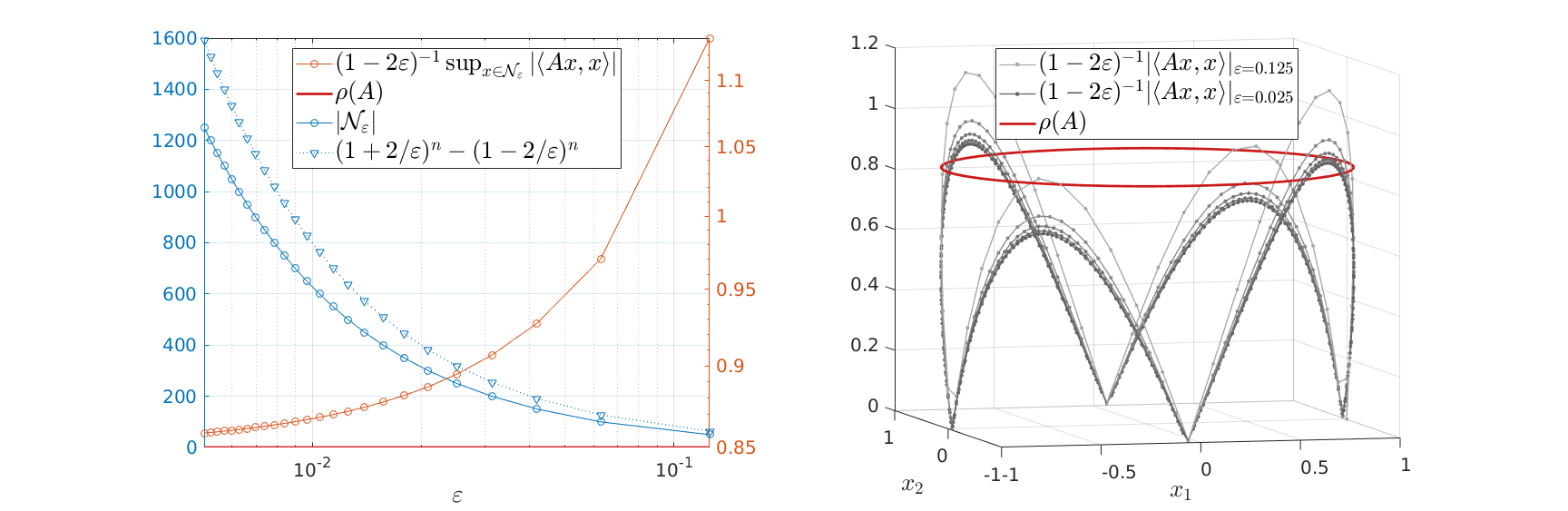 |
Overall, we see that after about a 100 calls to our oracle we can be sure about  being exponentially stable.
Here we just highlighted an example from (RV2011), at a later moment we will discuss its use in probability theory.
being exponentially stable.
Here we just highlighted an example from (RV2011), at a later moment we will discuss its use in probability theory.
Help the (skinny) Hedgehogs | 31 Oct. 2019 |
tags: math.LA
In this first post we will see that the ‘‘almost surely’’ in the title is not only hinting at stochasticity.
For a long time this picture - as taken from Gabriel Peyré his outstanding twitter feed - has been on a wall in our local wildlife (inc. hedgehogs) shelter. This has lead to a few fun discussions and here we try to explain the picture a bit more.
Let 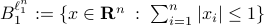 . Now, we want to find the largest ball
. Now, we want to find the largest ball 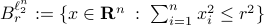 within
within 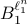 . We can find that
. We can find that  is given by
is given by 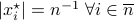 with
with 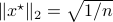 . This follows the most easily from geometric intuition.
. This follows the most easily from geometric intuition.
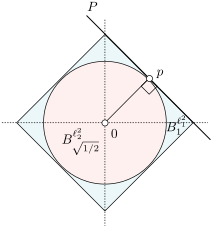 |
To prove it, see that |
Besides being a fun visualization of concentration, this picture means a bit more to me. For years I have been working at the Wildlife shelter in Delft and the moment has come where the lack of financial support from surrounding municipalities is becoming critical. As usual, this problem can be largely attributed to bureaucracy and the exorbitant amount of managers this world has. Nevertheless, the team in Delft and their colleagues around the country do a fantastic job in spreading the word (see Volkskrant, RTLnieuws). Lets hope Delft, and it neighbours, finally see value in protecting the local wildlife we still have.
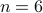 fair convex sets.
fair convex sets.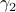 is usually much easier than dealing with
is usually much easier than dealing with 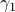 directly.
directly. 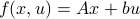 and
and 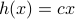 to the closest integer where
to the closest integer where ![[cdot]](eqs/8251583936328055799-130.png) , naive realization
, naive realization ![[sigma]](eqs/4713363484184404481-130.png) and to the optimized one
and to the optimized one ![[sigma^{star}]](eqs/5091401033446485837-130.png) .
We do 100 experiments and show the mean plus the full confidence interval (of the input-output behaviour), the optimized representation is remarkably better.
Numerically we observe that for
.
We do 100 experiments and show the mean plus the full confidence interval (of the input-output behaviour), the optimized representation is remarkably better.
Numerically we observe that for 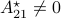 , which is precisely where the naive
, which is precisely where the naive  with
with 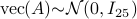 . When we compute the relative error
. When we compute the relative error 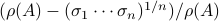 for
for 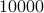 samples we obtain the histogram as shown on the left. Clearly, the relative error is not concentrated near
samples we obtain the histogram as shown on the left. Clearly, the relative error is not concentrated near 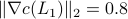 , which is still far from
, which is still far from 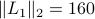 .
. 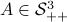 be given by
be given by 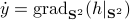 . We see that the gradient flow under the quadratic function takes a clearly ‘‘shorter’’ path.
. We see that the gradient flow under the quadratic function takes a clearly ‘‘shorter’’ path. 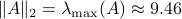 . Indeed, when given 100
. Indeed, when given 100 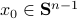 , we observe convergence. To apply this in practice we obviously need to discretize the flow. To add to that, if we consider the discrete-time version of
, we observe convergence. To apply this in practice we obviously need to discretize the flow. To add to that, if we consider the discrete-time version of 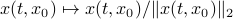 we can get something of the form
we can get something of the form 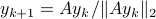 , which is indeed the
, which is indeed the 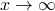 cannot even occur.
Let a great arc (circle)
cannot even occur.
Let a great arc (circle)  on
on  be parametrized by the normal of a hyperplane
be parametrized by the normal of a hyperplane 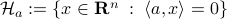 through
through 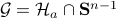 ,
, 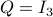 and let
and let 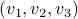 be
be 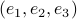 . Then using the procedure from before, we find that
. Then using the procedure from before, we find that 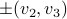 are locally unstable in one direction while
are locally unstable in one direction while 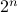 ‘‘similar’’ faces, without loss of generality we take the one in the positive orthant of
‘‘similar’’ faces, without loss of generality we take the one in the positive orthant of 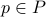 the closest (in
the closest (in 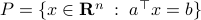 for
for 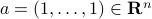 and
and 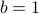 . Thus the normal (direction) is given by
. Thus the normal (direction) is given by  we have
we have 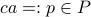 . Hence we have
. Hence we have 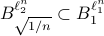 . Now, let
. Now, let 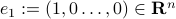 and define the other
and define the other 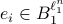 for any
for any 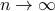 . The inscribed ball shrinks to
. The inscribed ball shrinks to