Riemannian Gradient Flow |5 Nov. 2019|
tags: math.DG, math.DS
Previously we looked at 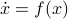 ,
, 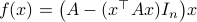 - and its resulting flow - as the result from mapping
- and its resulting flow - as the result from mapping 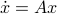 to the sphere. However, we saw that for
to the sphere. However, we saw that for 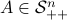 this flow convergences to
this flow convergences to 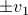 , with
, with 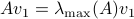 such that for
such that for 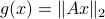 we have
we have 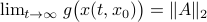
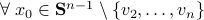 . Hence, it is interesting to look at the flow from an optimization point of view:
. Hence, it is interesting to look at the flow from an optimization point of view: 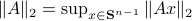 .
.
A fair question would be, is our flow not simply Riemannian gradient ascent for this problem? As common with these kind of problems, such a hypothesis is something you just feel.
Now, using the tools from (CU1994, p.311) we can compute the gradient of 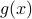 (on the sphere) via
(on the sphere) via 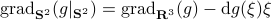 , where
, where 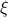 is a vector field normal to
is a vector field normal to 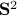 , e.g.,
, e.g., 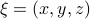 .
From there we obtain
.
From there we obtain
![mathrm{grad}_{mathbf{S}^2}(g|_{mathbf{S}^2}) = left[ begin{array}{lll} (1-x^2) & -xy & -xz -xy & (1-y^2) & -yz -xz & -yz & (1-z^2) end{array}right] left[ begin{array}{l}partial_x g partial_y g partial_z g end{array}right]=G(x,y,z)nabla g.](eqs/2499009703266316151-130.png)
To make our life a bit easier, use instead of 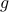 the map
the map 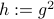 . Moreover, set
. Moreover, set 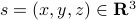 . Then it follows that
. Then it follows that
![begin{array}{ll} mathrm{grad}_{mathbf{S}^2}(h|_{mathbf{S}^2}) &= left(I_3-mathrm{diag}(s)left[begin{array}{l} s^{top}s^{top}s^{top} end{array}right]right) 2A^{top}As &= 2left(A^{top}A-(s^{top}A^{top}Asright)I_3)s. end{array}](eqs/2245781100057659571-130.png)
Of course, to make the computation cleaner, we changed 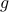 to
to 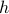 , but the relation between
, but the relation between 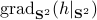 and
and  is beautiful. Somehow, mapping trajectories of
is beautiful. Somehow, mapping trajectories of 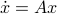 , for some
, for some 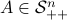 , to the sphere corresponds to (Riemannian) gradient ascent applied to the problem
, to the sphere corresponds to (Riemannian) gradient ascent applied to the problem 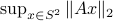 .
.
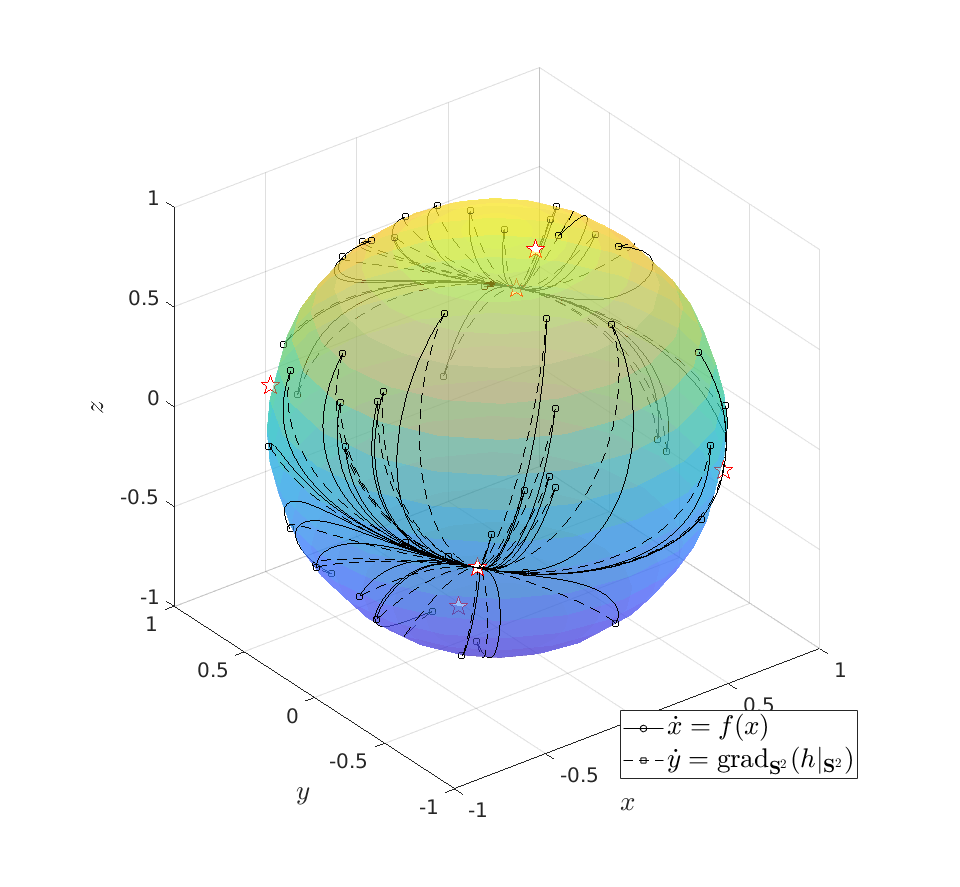 |
To do an example, let ![A = left[ begin{array}{lll} 10 & 2 & 0 2 & 10 & 2 0 & 2 & 1 end{array}right].](eqs/6133576945654762450-130.png)
We can compare |
Now, we formalize the previous analysis a bit and show how fast we converge. Assume that the eigenvectors are ordered such that eigenvector  corresponds to the largest eigenvalue of
corresponds to the largest eigenvalue of  . Then, the solution to
. Then, the solution to  is given by
is given by
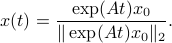
Let 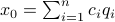 be
be 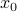 expressed in eigenvector coordinates, with all
expressed in eigenvector coordinates, with all 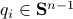 (normalized). Moreover, assume all eigenvalues are distinct. Then, to measure if
(normalized). Moreover, assume all eigenvalues are distinct. Then, to measure if 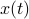 is near
is near 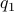 , we compute
, we compute 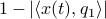 , which is
, which is  if and only if
if and only if 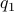 is parallel to
is parallel to 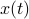 . To simplify the analysis a bit, we look at
. To simplify the analysis a bit, we look at 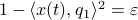 , for some perturbation
, for some perturbation 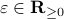 , this yields
, this yields
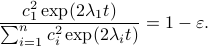
Next, take the the (natural) logarithm on both sides:
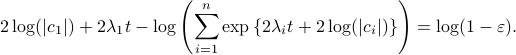
This log-sum-exp terms are hard to deal with, but we can apply the so-called ‘‘log-sum-exp trick’’:
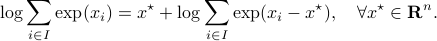
In our case, we set 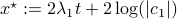 and obtain
and obtain
![-log left(sum^{n}_{i=1}exp left{2 left[(lambda_i-lambda_1)t + logleft(frac{|c_i|}{|c_1|} right) right] right}+1 right) = log(1-varepsilon).](eqs/3165375830294523712-130.png)
We clearly observe that for  the LHS approaches
the LHS approaches  from below, which means that
from below, which means that 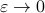 from above, like intended. Of course, we also observe that the mentioned method is not completely general, we already assume distinct eigenvalues, but there is more. We do also not convergence when
from above, like intended. Of course, we also observe that the mentioned method is not completely general, we already assume distinct eigenvalues, but there is more. We do also not convergence when 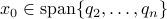 , which is however a set of measure
, which is however a set of measure  on the sphere
on the sphere 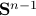 .
.
More interestingly, we see that the convergence rate is largely dictated by the ‘‘spectral gap/eigengap’’ 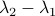 . Specifically, to have a particular projection error
. Specifically, to have a particular projection error  , such that
, such that 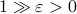 , we need
, we need
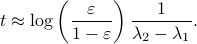
Comparing this to the resulting flow from 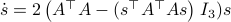 ,
,  , we see that we have the same flow, but with
, we see that we have the same flow, but with 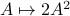 .
This is interesting, since
.
This is interesting, since  and
and 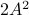 have the same eigenvectors, yet a different (scaled) spectrum. With respect to the convergence rate, we have to compare
have the same eigenvectors, yet a different (scaled) spectrum. With respect to the convergence rate, we have to compare 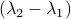 and
and 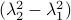 for any
for any 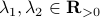 with
with 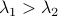 (the additional
(the additional  is not so interesting).
is not so interesting).
It is obvious what we will happen, the crux is, is 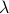 larger or smaller than
larger or smaller than  ? Can we immediately extend this to a Newton-type algorithm? Well, this fails (globally) since we work in
? Can we immediately extend this to a Newton-type algorithm? Well, this fails (globally) since we work in 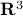 instead of purely with
instead of purely with 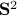 . To be concrete,
. To be concrete, 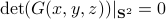 , we never have
, we never have 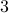 degrees of freedom.
degrees of freedom.
Of course, these observations turned out to be far from new, see for example (AMS2008, sec. 4.6).
(AMS2008) P.A. Absil, R. Mahony and R. Sepulchre: ‘‘Optimization Algorithms on Matrix Manifolds’’, 2008 Princeton University Press.
(CU1994) Constantin Udriste: ‘‘Convex Functions and Optimization Methods on Riemannian Manifolds’’, 1994 Kluwer Academic Publishers.
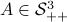 be given by
be given by 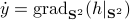 . We see that the gradient flow under the quadratic function takes a clearly ‘‘shorter’’ path.
. We see that the gradient flow under the quadratic function takes a clearly ‘‘shorter’’ path.